
分析 可在$\overrightarrow{c}=\overrightarrow{a}+m\overrightarrow{b}$的两边同乘以向量$\overrightarrow{c}$便可得出${\overrightarrow{c}}^{2}=\overrightarrow{a}•\overrightarrow{c}+m\overrightarrow{b}•\overrightarrow{c}$,而根据条件可得到${\overrightarrow{c}}^{2}=4,\overrightarrow{a}•\overrightarrow{c}=0,且\overrightarrow{b}•\overrightarrow{c}=-2$,带入上式即可求出m的值.
解答 解:在$\overrightarrow{c}=\overrightarrow{a}+m\overrightarrow{b}$两边同乘以$\overrightarrow{c}$得:
${\overrightarrow{c}}^{2}=\overrightarrow{a}•\overrightarrow{c}+m\overrightarrow{b}•\overrightarrow{c}$;
∵$\overrightarrow{a}⊥\overrightarrow{c}$;
∴$\overrightarrow{a}•\overrightarrow{c}=0$,且$\overrightarrow{b}•\overrightarrow{c}=-2,|\overrightarrow{c}|=2$;
∴4=0-2m;
∴m=-2.
故答案为:-2.
点评 考查向量数量积的运算及其计算公式,以及向量垂直的充要条件.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$海里 | B. | $\sqrt{3}$海里 | C. | 2$\sqrt{3}$海里 | D. | 3海里 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{7}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
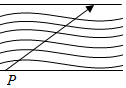 今有一小船位于宽d=60m的河边P处,从这里起,在下游l=80m处河流有一瀑布,若河水流速方向由上游指向下游(与河岸平行),水速大小为5m/s,如图,为了使小船能安全渡河,船的划速不能小于多少?当划速最小时,划速方向如何?(sin37°=$\frac{3}{5}$)
今有一小船位于宽d=60m的河边P处,从这里起,在下游l=80m处河流有一瀑布,若河水流速方向由上游指向下游(与河岸平行),水速大小为5m/s,如图,为了使小船能安全渡河,船的划速不能小于多少?当划速最小时,划速方向如何?(sin37°=$\frac{3}{5}$)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
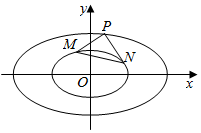 已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点A($\sqrt{2}$,0),且离心率e=$\frac{\sqrt{2}}{2}$.
已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点A($\sqrt{2}$,0),且离心率e=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com