
分析 由等差数列的前n项和公式化简已知两等式,联立求出首项a1与公差d的值,结合导数求出nSn的最小值.
解答 解:设等差数列{an}的首项为a1,公差为d,
∵S10=10a1+45d=0,S15=15a1+105d=25,
∴a1=-3,d=$\frac{2}{3}$,
∴Sn=na1+$\frac{n(n+1)}{2}$d=$\frac{1}{3}$n2-$\frac{10}{3}$n,
∴(n+1)Sn=$\frac{1}{3}$n3-$\frac{10}{3}$n2+$\frac{1}{3}$n2-$\frac{10}{3}$n=$\frac{1}{3}$n3-3n2-$\frac{10}{3}$n
令nSn=f(n),
∴f′(n)=n2-6n-$\frac{10}{3}$,
∴当n=$3+\frac{1}{3}\sqrt{37}$时,f(n)取得极值,当3$-\frac{1}{3}\sqrt{37}$<n<$3+\frac{1}{3}\sqrt{37}$时,f(n)递减;当n>$3+\frac{1}{3}\sqrt{37}$时,f(n)递增;
因此只需比较f(6)和f(7)的大小即可.
f(6)=-56,f(7)=-56,
故(n+1)Sn的最小值为-59.
故答案为:6或7.
点评 此题考查了等差数列的性质,以及等差数列的前n项和公式,函数的导数的应用,熟练掌握性质及公式是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
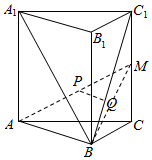 如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,AA1=2,AC=2$\sqrt{2}$,M是CC1的中点,P是AM的中点,点Q在线段BC1上,且BQ=$\frac{1}{3}$QC1.
如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,AA1=2,AC=2$\sqrt{2}$,M是CC1的中点,P是AM的中点,点Q在线段BC1上,且BQ=$\frac{1}{3}$QC1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
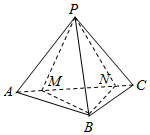 如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,AB=BC=PA=PC=2,M,N为线段AC上的点,若MN=2,则三棱锥P-MNB的体积为( )
如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,AB=BC=PA=PC=2,M,N为线段AC上的点,若MN=2,则三棱锥P-MNB的体积为( )| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
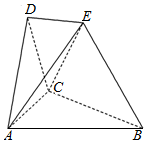 在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成角为60°,且点E在平面ABC上射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成角为60°,且点E在平面ABC上射影落在∠ABC的平分线上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
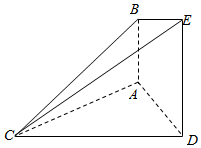 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB.
如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A′B′C′中,AA′=2AC=2BC,E为AA′的中点,C′E⊥BE.
如图,直三棱柱ABC-A′B′C′中,AA′=2AC=2BC,E为AA′的中点,C′E⊥BE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com