
分析 (1)若甲、乙比赛4局甲获胜,则甲在4局比赛中至少胜3局,由此能求出P(2),同理能求出P(3)的值.
(2)在2n局比赛中甲获胜,则甲胜的局数至少为n+1局,从而$P({n+1})=\frac{1}{2}({1-\frac{{C_{2n+2}^{n+1}}}{{{2^{2n+2}}}}})$,由此能求出P(n)<P(n+1).
解答 解:(1)若甲、乙比赛4局甲获胜,则甲在4局比赛中至少胜3局,
所以$P(2)=C_4^3{({\frac{1}{2}})^4}+C_4^4{({\frac{1}{2}})^4}=\frac{5}{16}$,
同理$P(3)=C_6^4{({\frac{1}{2}})^6}+C_6^5{({\frac{1}{2}})^6}+C_6^6{({\frac{1}{2}})^6}=\frac{11}{32}$.
(2)在2n局比赛中甲获胜,则甲胜的局数至少为n+1局,
故$P(n)=C_{2n}^{n+1}{({\frac{1}{2}})^{2n}}+C_{2n}^{n+2}{({\frac{1}{2}})^{2n}}+…+C_{2n}^{2n}{({\frac{1}{2}})^{2n}}$=$({C_{2n}^{n+1}+C_{2n}^{n+2}+…+C_{2n}^{2n}})•{({\frac{1}{2}})^{2n}}=\frac{1}{2}({{2^{2n}}-C_{2n}^n})•{({\frac{1}{2}})^{2n}}=\frac{1}{2}({1-\frac{{C_{2n}^n}}{{{2^{2n}}}}})$,
所以$P({n+1})=\frac{1}{2}({1-\frac{{C_{2n+2}^{n+1}}}{{{2^{2n+2}}}}})$,
又因为$\frac{{\frac{{C_{2n}^n}}{{{2^{2n}}}}}}{{\frac{{C_{2n+2}^{n+1}}}{{{2^{2n+2}}}}}}=\frac{{4C_{2n}^n}}{{C_{2n+2}^{n+1}}}=\frac{{4\frac{{({2n})!}}{n!n!}}}{{\frac{{({2n+2})!}}{{({n+1})!({n+1})!}}}}=\frac{{4{{({n+1})}^2}}}{{({2n+2})({2n+1})}}=\frac{{2({n+1})}}{2n+1}>1$,
所以$\frac{{C_{2n}^n}}{{{2^{2n}}}}>\frac{{C_{2n+2}^{n+1}}}{{{2^{2n+2}}}}$,所以P(n)<P(n+1).
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意n次独立重复试验中事件A恰好发生k次的概率计算公式的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有两个数是正数 | B. | 至少有两个数是正数 | ||
| C. | 至少有两个数是负数 | D. | 这三个数都是正数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 12 | C. | 14 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$海里 | B. | $\sqrt{3}$海里 | C. | 2$\sqrt{3}$海里 | D. | 3海里 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
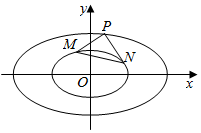 已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点A($\sqrt{2}$,0),且离心率e=$\frac{\sqrt{2}}{2}$.
已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点A($\sqrt{2}$,0),且离心率e=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com