
| A. | 10 | B. | 12 | C. | 14 | D. | 15 |
分析 如图所示,设椭圆的左焦点为F′,|AF|=$\sqrt{{2}^{2}+(2\sqrt{3})^{2}}$=4=|AF′|,|PF|+|PF′|=2a=6,利用|PA|-|PF′|≤|AF′|,即可得出.
解答 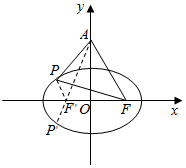 解:如图所示设椭圆的左焦点为F′,
解:如图所示设椭圆的左焦点为F′,
|AF|=$\sqrt{{2}^{2}+(2\sqrt{3})^{2}}$=4=|AF′|,
则|PF|+|PF′|=2a=6,
∵|PA|-|PF′|≤|AF′|,
∴△APF的周长=|AF|+|PA|+|PF|=|AF|+|PA|+6-|PF′|≤4+6+4=14,当且仅当三点A,F′,P共线时取等号.
∴△APF的周长最大值等于14.
故选:C.
点评 本题考查了椭圆的定义标准方程及其性质、三角形三边大小关系,考查了数形结合方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
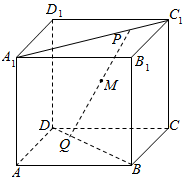 在长方体ABCD-A1B1C1D1中,AB=3,AD=4,AA1=5,点P、Q分别在直线A1C1和BD上运动,且PQ=8,则PQ的中点M的轨迹是( )
在长方体ABCD-A1B1C1D1中,AB=3,AD=4,AA1=5,点P、Q分别在直线A1C1和BD上运动,且PQ=8,则PQ的中点M的轨迹是( )| A. | 平行四边形 | B. | 圆 | C. | 椭圆 | D. | 非以上图形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
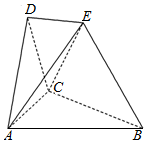 在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成角为60°,且点E在平面ABC上射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成角为60°,且点E在平面ABC上射影落在∠ABC的平分线上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A′B′C′中,AA′=2AC=2BC,E为AA′的中点,C′E⊥BE.
如图,直三棱柱ABC-A′B′C′中,AA′=2AC=2BC,E为AA′的中点,C′E⊥BE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ln2-1 | B. | ln2-2 | C. | 2ln2-1 | D. | 2ln2-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com