
分析 (Ⅰ)根据正弦定理、两角和的正弦公式化简已知的式子,求出tanA,由内角的范围求出A;
(Ⅱ)根据二倍角的余弦公式变形化简解析式,由周期公式求出ω的值,由x的范围和余弦函数的性质求出求函数f(x)值域.
解答 解:(Ⅰ)∵$asinB+\sqrt{3}acosB=\sqrt{3}c$,
∴$sinAsinB+\sqrt{3}sinAcosB=\sqrt{3}sinC$…(2分)
∵C=π-(A+B),
∴$sinAsinB+\sqrt{3}sinAcosB=\sqrt{3}sin(A+B)$=$\sqrt{3}(sinAcosB+cosAsinB)$,
则$sinAsinB=\sqrt{3}cosAsinB$,
∵sinB≠0,∴$tanA=\sqrt{3}$,
由0<A<π得,$A=\frac{π}{3}$.…(6分)
(Ⅱ)$f(x)=5co{s}^{2}(ωx+\frac{π}{6})-3$=$\frac{5}{2}[1+cos(2ωx+\frac{π}{3})]-3$
=$\frac{5}{2}cos(2ωx+\frac{π}{3})-\frac{1}{2}$,
∴$g(x)=\frac{5}{2}cos(\frac{4}{3}ωx+\frac{π}{3})-\frac{1}{2}$,
∴$\frac{2π}{\frac{4}{3}ω}=π$,解得$ω=\frac{3}{2}$,
即$f(x)=\frac{5}{2}cos(3x+\frac{π}{3})-\frac{1}{2}$,…(9分)
由$x∈[0,\frac{π}{3}]$得,$\frac{π}{3}≤3x+\frac{π}{3}≤\frac{4}{3}π$,∴$-1≤cos(3x+\frac{π}{3})≤\frac{1}{2}$,
即$-3≤f(x)≤\frac{3}{4}$,∴f(x)的值域为$[-3,\frac{3}{4}]$.…(12分)
点评 本题考查正弦定理,两角和的正弦公式、二倍角的余弦公式变形,以及余弦函数的性质,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 有两个数是正数 | B. | 至少有两个数是正数 | ||
| C. | 至少有两个数是负数 | D. | 这三个数都是正数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 12 | C. | 14 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$海里 | B. | $\sqrt{3}$海里 | C. | 2$\sqrt{3}$海里 | D. | 3海里 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x2 | B. | y=$\frac{2}{x}$ | C. | y=x-$\frac{1}{x}$ | D. | y=sin$\frac{π}{3}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{7}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
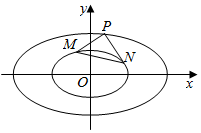 已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点A($\sqrt{2}$,0),且离心率e=$\frac{\sqrt{2}}{2}$.
已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点A($\sqrt{2}$,0),且离心率e=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com