
分析 先根据分组分配的方法求出所有的种数,再求出甲乙两同学恰好一起在第一周或第四周周末去养老院种数,根据概率公式计算即可.
解答 解:6位同学,决定分成四组,有(3,1,1,1)和(2,2,1,1)两种,
当为(3,1,1,1)有C63=20种,当为(2,2,1,1)有$\frac{{C}_{6}^{2}{C}_{4}^{2}{C}_{2}^{1}{C}_{1}^{1}}{{A}_{2}^{2}{A}_{2}^{2}}$=45种,
共分组的方法为20+45=65种,再分配到周一到周四,故有65A44=1560种,
其中甲乙两同学恰好一起的分组方法有C41+C42=10种,其中甲乙两同学恰好一起在第一周或第四周周末去养老院的有10C21A33=120种,
故甲乙两同学恰好一起在第一周或第四周周末去养老院的概率为$\frac{120}{1560}$=$\frac{1}{13}$,
故答案为:$\frac{1}{13}$
点评 本题考查了分组分配问题和古典概率的问题,关键分组,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 720 | B. | 840 | C. | 960 | D. | 1080 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
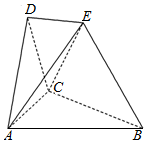 在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成角为60°,且点E在平面ABC上射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成角为60°,且点E在平面ABC上射影落在∠ABC的平分线上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
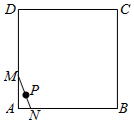 如图所示,有一条长度为1的线段MN,其端点M,N在边长为3的正方形ABCD的四边上滑动,当点N绕着正方形的四边滑动一周时,MN的中点P所形成轨迹的长度为( )
如图所示,有一条长度为1的线段MN,其端点M,N在边长为3的正方形ABCD的四边上滑动,当点N绕着正方形的四边滑动一周时,MN的中点P所形成轨迹的长度为( )| A. | $8+\frac{π}{2}$ | B. | 8+π | C. | $12+\frac{π}{2}$ | D. | 12+π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)=$\frac{8}{3}$ | B. | g(1)=$\frac{10}{3}$ | C. | 若a>b,则f(a)>f(b) | D. | 若a>b,则g(a)>g(b) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com