【题目】已知
.
（Ⅰ）若
在
是单调递增函数，求实数
的取值范围；
（Ⅱ）令
，若函数
有两个零点，求实数
的取值范围.
【答案】（Ⅰ）
;（Ⅱ）
．
【解析】试题分析：（Ⅰ） 
在
是单调递增函数,等价于
在
上恒成立，再转化为
，求最值即可.
（Ⅱ）
有两个零点，可转化为
，有两个交点问题，用导数研究函数的增减变化情况即可.
试题解析：（Ⅰ）由题意知
，
．
在
是单调递增函数
在
上恒成立
，
．
（Ⅱ）由题意知
，
由
，
令
，
，
由于
，可知
，
当
时， 
；当
时， 
，
故
在
上是单调减函数，
在
上是单调增函数，所以
，
函数
有两个零点
，
因此实数a的取值范围是
．
点晴:本题考查函数导数与单调性.确定零点的个数问题：可利用数形结合的办法判断交点个数，如果函数较为复杂，可结合导数知识确定极值点和单调区间从而确定其大致图象.方程的有解问题就是判断是否存在零点的问题，可参变分离，转化为求函数的值域问题处理. 恒成立问题以及可转化为恒成立问题的问题，往往可利用参变分离的方法，转化为求函数最值处理．也可构造新函数然后利用导数来求解.注意利用数形结合的数学思想方法.
优翼小帮手同步口算系列答案科目：高中数学 来源： 题型：
【题目】已知函数f（x）=sin（ωx+φ）﹣b（ω＞0，0＜φ＜π）的图象两相邻对称轴之间的距离是 
，若将f（x）的图象先向右平移 
个单位，再向上平移 
个单位，所得函数g（x）为奇函数．
（1）求f（x）的解析式；
（2）求f（x）的对称轴及单调区间；
（3）若对任意x∈[0， 
]，f2（x）﹣（2+m）f（x）+2+m≤0恒成立，求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】国内，某知名连接店分店开张营业期间，在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动，随着抽奖的有效展开，参与抽奖活动的人数越来越多，该分店经理对开业前7天参加抽奖活动的人数进行统计， 
表示开业第
天参加抽奖活动的人数，得到统计表格如下：
经过进一步的统计分析，发现
与
具有线性相关关系.
（1）如从这7天中随便机抽取两天，求至少有1天参加抽奖人数超过10天的概率；
（2）根据上表给出的数据，用最小二乘法，求出
与
的线性回归方程
，并估计若该活动持续10天，共有多少名顾客参加抽奖.
参考公式：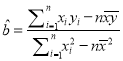 
， 
， 
， 
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】袋子中放有大小和形状相同的小球若干，其中标号为0的小球1个，标号为1的小球1个，标号为2的小球2个.从袋子中不放回地随机抽取小球两个，每次抽取一个球，记第一次取出的小球标号为
，第二次取出的小球标号为
.
（1）记事件
表示“
”，求事件的概率；
（2）在区间
内任取两个实数
，
，求“事件
恒成立”的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知：以点C（t， 
）（t∈R，t≠0）为圆心的圆与x轴交于点O，A，与y轴交于点O，B，其中O为原点．
（1）当t=2时，求圆C的方程；
（2）求证：△OAB的面积为定值；
（3）设直线y=﹣2x+4与圆C交于点M，N，若|OM|=|ON|，求圆C的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}的前n项和为Sn，且Sn=2n2+n，n∈N，数列{bn}满足an=4log2bn+3，n∈N．
（1）求an，bn；
（2）求数列{anbn}的前n项和Tn．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
