
【题目】已知数集![]() 具有性质
具有性质![]() ;对任意的
;对任意的![]() 、
、![]() ,
,![]() ,与
,与![]() 两数中至少有一个属于
两数中至少有一个属于![]() .
.
(1)分别判断数集![]() 与
与![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)证明:![]() ,且
,且![]() ;
;
(3)当![]() 时,若
时,若![]() ,求集合
,求集合![]() .
.
【答案】(1) 集合![]() 具有性质
具有性质![]() ,集合
,集合![]() 不具有性质
不具有性质![]() .(2)证明见解析.(3)
.(2)证明见解析.(3)![]() .
.
【解析】
(1)利用![]() 与
与![]() 两数中至少有一个属于
两数中至少有一个属于![]() .即可判断出结论.
.即可判断出结论.
(2)令“![]() ,由“
,由“![]() 与
与![]() 两数中至少有一个属于
两数中至少有一个属于![]() ”可得
”可得![]() 属于
属于![]() .
.
令![]() ,那么
,那么![]() 是集合
是集合![]() 中某项,
中某项,![]() 不符合不符合题意,
不符合不符合题意,![]() 符合.同理可得:令
符合.同理可得:令![]() 可以得到
可以得到![]() ,令
,令![]() ,
,![]() 可以得到
可以得到![]() ,倒序相加即可.
,倒序相加即可.
(3)当![]() 时,取
时,取![]() ,当
,当![]() 时,
时,![]() ,由A具有性质P,
,由A具有性质P,![]() ,又
,又![]() 时,
时,![]() ,可得
,可得![]()
![]() ,则
,则![]() ,又
,又![]() ,可得
,可得![]() ,则
,则![]() ,则有
,则有![]() .可得即
.可得即![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 等差数列是首项为0,公差为
等差数列是首项为0,公差为![]() 等差数列.
等差数列.
解:(1)在集合![]() 中,设
中,设![]()
①![]() ,具有性质
,具有性质![]()
②![]() ,具有性质
,具有性质![]()
③![]() ,具有性质
,具有性质![]()
④![]() ,具有性质
,具有性质![]()
⑤![]() ,具有性质
,具有性质![]()
⑥![]() ,具有性质
,具有性质![]()
综上所述:集合![]() 具有性质
具有性质![]() ;
;
在集合![]() 中,设
中,设![]() ,
,
①![]() ,具有性质
,具有性质![]()
②![]() ,具有性质
,具有性质![]()
③![]() ,具有性质
,具有性质![]()
④![]() ,不具有性质
,不具有性质![]()
⑤![]() ,具有性质
,具有性质![]()
⑥![]() ,具有性质
,具有性质![]()
综上所述:集合![]() 不具有性质
不具有性质![]() .
.
故集合![]() 具有性质
具有性质![]() ,集合
,集合![]() 不具有性质
不具有性质![]() .
.
(2) 证明:令![]()
![]() ,
,
则![]() 与
与![]() 两数中至少有一个属于
两数中至少有一个属于![]() ”,
”,
![]() 不属于
不属于![]() ,
,![]() 属于
属于![]() .
.
令![]() ,那么
,那么![]() 是集合
是集合![]() 中某项,
中某项,![]() 不符合题意,
不符合题意,![]() 可以.
可以.
如果是![]() 或者
或者![]() ,那么可知
,那么可知![]() ,
,
那么![]() ,只能是等于
,只能是等于![]() ,矛盾.
,矛盾.
所以令![]() 可以得到
可以得到![]() ,
,
同理,令![]() ,
,![]() 可以得到
可以得到![]() ,
,
![]() 倒序相加即可得到
倒序相加即可得到![]()
即![]()
(3)当![]() 时,取
时,取![]() ,当
,当![]() 时,
时,![]() ,
,
由![]() 具有性质
具有性质![]() ,
,![]() ,又
,又![]() 时,
时,![]() ,
,
![]()
![]() ,
,
![]() ,
,
则![]() ,
,
![]() ,
,
从而可得![]() ,
,
故![]() ,即
,即![]() ,
,
又![]()
![]()
,则![]() ,则有
,则有![]()
又![]()
![]() ,
,
即![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 等差数列,
等差数列,
![]()


科目:高中数学 来源: 题型:
【题目】现有一块大型的广告宣传版面,其形状是右图所示的直角梯形![]() .某厂家因产品宣传的需要,拟投资规划出一块区域(图中阴影部分)为产品做广告,形状为直角梯形
.某厂家因产品宣传的需要,拟投资规划出一块区域(图中阴影部分)为产品做广告,形状为直角梯形![]() (点
(点![]() 在曲线段
在曲线段![]() 上,点
上,点![]() 在线段
在线段![]() 上).已知
上).已知![]() ,
, ![]() ,其中曲线段
,其中曲线段![]() 是以
是以![]() 为顶点,
为顶点, ![]() 为对称轴的抛物线的一部分.
为对称轴的抛物线的一部分.
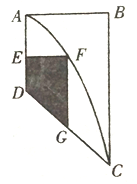
(1)建立适当的平面直角坐标系,分别求出曲线段![]() 与线段
与线段![]() 的方程;
的方程;
(2)求该厂家广告区域![]() 的最大面积.
的最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,
, ![]() 上的动点
上的动点![]() 到两焦点的距离之和为4,当点
到两焦点的距离之和为4,当点![]() 运动到椭圆
运动到椭圆![]() 的上顶点时,直线
的上顶点时,直线![]() 恰与以原点
恰与以原点![]() 为圆心,以椭圆
为圆心,以椭圆![]() 的离心率为半径的圆相切.
的离心率为半径的圆相切.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的左右顶点分别为
的左右顶点分别为![]() ,若
,若![]() 交直线
交直线![]() 于
于![]() 两点.问以
两点.问以![]() 为直径的圆是否过定点?若过定点,请求出该定点坐标;若不过定点,请说明理由.
为直径的圆是否过定点?若过定点,请求出该定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中生调查了当地某小区的50户居民由于台风造成的经济损失,将收集的数据分成![]() 三组,并作出如下频率分布直方图:
三组,并作出如下频率分布直方图:

(1)在直方图的经济损失分组中,以各组的区间中点值代表该组的各个值,并以经济损失落入该区间的频率作为经济损失取该区间中点值的概率(例如:经济损失![]() 则取
则取![]() ,且
,且![]() 的概率等于经济损失落入
的概率等于经济损失落入![]() 的频率)。现从当地的居民中随机抽出2户进行捐款援助,设抽出的2户的经济损失的和为
的频率)。现从当地的居民中随机抽出2户进行捐款援助,设抽出的2户的经济损失的和为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
(2)台风后居委会号召小区居民为台风重灾区捐款,此高中生调查的50户居民捐款情况如下表,在表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
捐款超过500元 | 30 | ||
捐款不超过500元 | 6 | ||
合计 |
附:临界值表参考公式:  .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的内接等边三角形
的内接等边三角形![]() 的面积为
的面积为![]() (其中
(其中![]() 为坐标原点).
为坐标原点).
(1)试求抛物线![]() 的方程;
的方程;
(2)已知点![]() 两点在抛物线
两点在抛物线![]() 上,
上,![]() 是以点
是以点![]() 为直角顶点的直角三角形.
为直角顶点的直角三角形.
①求证:直线![]() 恒过定点;
恒过定点;
②过点![]() 作直线
作直线![]() 的垂线交
的垂线交![]() 于点
于点![]() ,试求点
,试求点![]() 的轨迹方程,并说明其轨迹是何种曲线.
的轨迹方程,并说明其轨迹是何种曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:
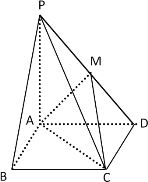
【题目】如图,在四棱锥P-ABCD中,底面ABCD是矩形, M为PD的中点,PA⊥平面ABCD,PA=AD= 4, AB = 2.
(1)求证:AM⊥平面MCD;
(2)求直线PC与平面MAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计划在某水库建一座至多安装4台发电机的水电站,过去0年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和,单位:亿立方米)都在40以上,其中,不足80的年份有10年,不低于80且不足120的年份有30年,不低于120且不足160的年份有8年,不低于160的年份有2年,将年入流量在以上四段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和,单位:亿立方米)都在40以上,其中,不足80的年份有10年,不低于80且不足120的年份有30年,不低于120且不足160的年份有8年,不低于160的年份有2年,将年入流量在以上四段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求在未来3年中,至多1年的年入流量不低于120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 的限制,并有如下关系:
的限制,并有如下关系:
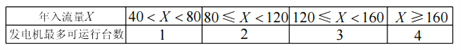
若某台发电机运行,则该台发电机年利润为500万元;若某台发电机未运行,则该台发电机年亏损1500万元,水电站计划在该水库安装2台或3台发电机,你认为应安装2台还是3台发电机?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x(年)和所支出的维修费用y(万元)有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)画出散点图并判断是否线性相关;
(2)如果线性相关,求线性回归方程;
(3)估计使用年限为10年时,维修费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com