
分析 (1)运用同角的平方关系,可得曲线C的普通方程;再由x=ρcosθ,y=ρsinθ,代入普通方程,可得极坐标方程;
(2)设A(ρ1,θ),B(ρ2,θ-$\frac{π}{2}$),代入极坐标方程,由诱导公式和两角和的正弦公式,借助正弦函数的值域即可得到所求范围.
解答 解:(1)曲线C的参数方程是$\left\{\begin{array}{l}{x=1+2cosα}\\{y=\sqrt{3}sinα}\end{array}\right.$ (α∈R,α为参数),
由cos2α+sin2α=1,可得曲线C的普通方程为$\frac{(x-1)^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,
由x=ρcosθ,y=ρsinθ,可得3(ρcosθ-1)2+4ρ2sin2θ=12,
ρ2(3+sin2θ)-6ρcosθ-9=0,
解得ρ=$\frac{6cosθ±12}{2(3+si{n}^{2}θ)}$,
即有ρ=$\frac{3cosθ+6}{3+si{n}^{2}θ}$=$\frac{3(2+cosθ)}{4-co{s}^{2}θ}$=$\frac{3}{2-cosθ}$;
(2)点A,B在曲线C上,且∠AOB=90°,可设
A(ρ1,θ),B(ρ2,θ-$\frac{π}{2}$),
则$\frac{1}{|OA|}$+$\frac{1}{|OB|}$=$\frac{1}{{ρ}_{1}}$+$\frac{1}{{ρ}_{2}}$=$\frac{2-cosθ}{3}$+$\frac{2-cos(θ-\frac{π}{2})}{3}$
=$\frac{4-(sinθ+cosθ)}{3}$=$\frac{4-\sqrt{2}sin(θ+\frac{π}{4})}{3}$,
当sin(θ+$\frac{π}{4}$)=1时,上式取得最小值$\frac{4-\sqrt{2}}{3}$;
当sin(θ+$\frac{π}{4}$)=-1时,上式取得最大值$\frac{4+\sqrt{2}}{3}$.
故$\frac{1}{|OA|}$+$\frac{1}{|OB|}$的取值范围是[$\frac{4-\sqrt{2}}{3}$,$\frac{4+\sqrt{2}}{3}$].
点评 本题考查参数方程、极坐标方程和普通方程的转化,注意运用同角的平方关系和极坐标与直角坐标的关系,考查两角和的正弦公式和正弦函数的值域的运用,考查运算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
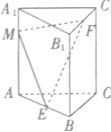 如图,已知ABC-A1B1C1是所有棱长均相等的正三棱柱,点E是棱AB的中点,点F是棱B1C1的中点,点M是棱AA1上的动点,则二面角B1-EM-F的正切值不可能等于( )
如图,已知ABC-A1B1C1是所有棱长均相等的正三棱柱,点E是棱AB的中点,点F是棱B1C1的中点,点M是棱AA1上的动点,则二面角B1-EM-F的正切值不可能等于( )| A. | $\frac{\sqrt{15}}{6}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{5}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{41}$ | B. | $\sqrt{39}$ | C. | 6 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在单位正方体ABCD-A1B1C1D1中,O是B1D1的中点,如图建立空间直角坐标系.
在单位正方体ABCD-A1B1C1D1中,O是B1D1的中点,如图建立空间直角坐标系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com