
【题目】给出下列四个命题:
①函数![]() ,
,![]() 的图象与直线
的图象与直线![]() 可能有两个不同的交点;
可能有两个不同的交点;
②函数![]() 与函数
与函数![]() 是相等函数;
是相等函数;
③对于指数函数![]() 与幂函数
与幂函数![]() ,总存在
,总存在![]() ,当
,当![]() 时,有
时,有![]() 成立;
成立;
④已知![]() 是方程
是方程![]() 的根,
的根,![]() 是方程
是方程![]() 的根,则
的根,则![]() .
.
其中正确命题的序号是__________.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+![]() ,且此函数的图象过点(1,5).
,且此函数的图象过点(1,5).
(1)求实数m的值并判断f(x)的奇偶性;
(2)判断函数f(x)在[2,+∞)上的单调性,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产一种机器的固定成本为0.5万元,但每生产100台,需要加可变成本(即另增加投入)0.25万元,市场对此产品的年求量为500台,销售的收入函数为![]() (万元)(
(万元)(![]() ),其中
),其中![]() 是产品售出的数量(单位:百台).
是产品售出的数量(单位:百台).
(1)把利润表示为年产量的函数;
(2)年产量是多少时,工厂所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是新中国成立70周年,也是全面建成小康社会的关键之年.为喜迎祖国70周年生日,全民齐心奋力建设小康社会,某校特举办“喜迎国庆,共建小康”知识竞赛活动.下面的茎叶图是参赛两组选手的答题得分情况,则下列说法正确的是( )
甲 | 乙 | |||||
5 | 7 | 7 | ||||
7 | 3 | 2 | 8 | 3 | 4 | 5 |
3 | 9 | 1 | ||||
A.甲组选手得分的平均数小于乙组选手得分的平均数.
B.甲组选手得分的中位数大于乙组选手得分的平均数.
C.甲组选手得分的中位数等于乙组选手得分的中位数.
D.甲组选手得分的方差大于乙组选手得分的方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
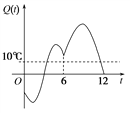
【题目】某地一年的气温Q(t)(单位:℃)与时间t(月份)之间的关系如图所示,已知该年的平均气温为10 ℃,令C(t)表示时间段[0,t]的平均气温,下列四个函数图象中,最能表示C(t)与t之间的函数关系的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() (a>0,b>0)的左焦点为F(-c,0)(c>0),过点F作圆x2+y2=
(a>0,b>0)的左焦点为F(-c,0)(c>0),过点F作圆x2+y2=![]() 的一条切线交圆于点E,交双曲线右支于点P,若
的一条切线交圆于点E,交双曲线右支于点P,若![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. ![]() B.
B. ![]()
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,![]() 分别是
分别是![]() 的中点,将四边形
的中点,将四边形![]() ,
,![]() 分别沿
分别沿![]() ,
,![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,如图2所示,
,如图2所示,![]() 是
是![]() 上一点,且
上一点,且![]() .
.

(1)求证:![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com