
分析 (I)t=2时,命题p中的双曲线为:$\frac{{y}^{2}}{2}-\frac{{x}^{2}}{6}$=1,可得a=$\sqrt{2}$,b=$\sqrt{6}$,c=2$\sqrt{2}$.即可得出e=$\frac{c}{a}$,其渐近线方程为y=$±\frac{a}{b}$x.
(II)命题p:方程$\frac{{y}^{2}}{4-t}$+$\frac{{x}^{2}}{t-8}$=1表示焦点在y轴上的双曲线,$\left\{\begin{array}{l}{4-t>0}\\{t-8<0}\end{array}\right.$,解得t,可得¬p:t≥4,令A=[4,+∞);
命题q:实数t使函数f(x)=log2(x2-2tx+2t+3)的定义域是R,可得x2-2tx+2t+3>0对于x∈R恒成立,因此△<0,解得t.可得:¬q,令B=(-∞,-1]∪[3,+∞).即可判断出结论.
解答 解:(I)t=2时,命题p中的双曲线为:$\frac{{y}^{2}}{2}-\frac{{x}^{2}}{6}$=1,∴a2=2,b2=6,c2=a2+b2=8,∴a=$\sqrt{2}$,b=$\sqrt{6}$,c=2$\sqrt{2}$.∴e=$\frac{c}{a}$=2,其渐近线方程为y=$±\frac{\sqrt{3}}{3}$x.
(II)命题p:方程$\frac{{y}^{2}}{4-t}$+$\frac{{x}^{2}}{t-8}$=1表示焦点在y轴上的双曲线,$\left\{\begin{array}{l}{4-t>0}\\{t-8<0}\end{array}\right.$,解得t<4,¬p:t≥4,令A=[4,+∞);
命题q:实数t使函数f(x)=log2(x2-2tx+2t+3)的定义域是R,∴x2-2tx+2t+3>0对于x∈R恒成立,∴△=4t2-4(2t+3)<0,解得-1<t<3.
∴¬q:t≤-1,或t≥3.令B=(-∞,-1]∪[3,+∞).
∵A?B,
∴命题¬p是命题¬q的充分不必要条件.
点评 本题考查了双曲线的标准方程及其性质、对数函数的性质、二次函数的性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
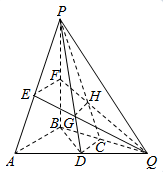 如图所示,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.
如图所示,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5海里 | B. | 5$\sqrt{2}$海里 | C. | 10海里 | D. | 10$\sqrt{2}$海里 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p∨q | B. | ¬p∧¬q | C. | p∧¬q | D. | p∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
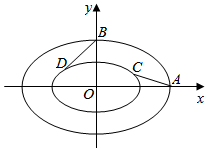 如图,内外两个椭圆的离心率相同,从外层椭圆顶点向内层椭圆引切线AC、BD,设内层椭圆方程$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),若直线AC与BD的斜率之积为-$\frac{1}{4}$,则椭圆的离心率为$\frac{{\sqrt{3}}}{2}$.
如图,内外两个椭圆的离心率相同,从外层椭圆顶点向内层椭圆引切线AC、BD,设内层椭圆方程$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),若直线AC与BD的斜率之积为-$\frac{1}{4}$,则椭圆的离心率为$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
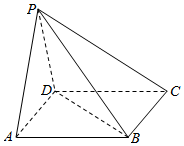 如图,在四棱锥P-ABCD中,底面四边形ABCD是边长为1的正方形,PA=PD,且PA⊥CD.
如图,在四棱锥P-ABCD中,底面四边形ABCD是边长为1的正方形,PA=PD,且PA⊥CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com