
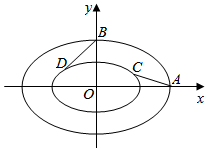
 如图,内外两个椭圆的离心率相同,从外层椭圆顶点向内层椭圆引切线AC、BD,设内层椭圆方程$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),若直线AC与BD的斜率之积为-$\frac{1}{4}$,则椭圆的离心率为$\frac{{\sqrt{3}}}{2}$.
如图,内外两个椭圆的离心率相同,从外层椭圆顶点向内层椭圆引切线AC、BD,设内层椭圆方程$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),若直线AC与BD的斜率之积为-$\frac{1}{4}$,则椭圆的离心率为$\frac{{\sqrt{3}}}{2}$. 分析 由于内层椭圆和外层椭圆的离心率相等,不妨设外层椭圆的方程为$\frac{{x}^{2}}{(ma)^{2}}+\frac{{y}^{2}}{(mb)^{2}}$=1,设切线AC的方程为y=k1(x-ma),代入椭圆方程消去y得:$({k}_{1}^{2}{a}^{2}+{b}^{2})$x2-2m${k}_{1}^{2}{a}^{3}$x+${m}^{2}{k}_{1}^{2}{a}^{4}$-a2b2=0,由△=0,化简得:${k}_{1}^{2}$=$\frac{{b}^{2}}{{a}^{2}}$$•\frac{1}{{m}^{2}-1}$,同理可得${k}_{2}^{2}$=$\frac{{b}^{2}}{{a}^{2}}•({m}^{2}-1)$,利用${k}_{1}^{2}{k}_{2}^{2}$=$\frac{{b}^{4}}{{a}^{4}}$=$(-\frac{1}{4})^{2}$,可得$\frac{b}{a}$=$\frac{1}{2}$,即可得出椭圆的离心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$.
解答 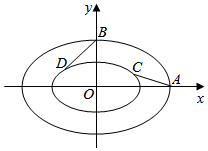 解:由于内层椭圆和外层椭圆的离心率相等,不妨设外层椭圆的方程为$\frac{{x}^{2}}{(ma)^{2}}+\frac{{y}^{2}}{(mb)^{2}}$=1,
解:由于内层椭圆和外层椭圆的离心率相等,不妨设外层椭圆的方程为$\frac{{x}^{2}}{(ma)^{2}}+\frac{{y}^{2}}{(mb)^{2}}$=1,
设切线AC的方程为y=k1(x-ma),代入椭圆方程消去y得:$({k}_{1}^{2}{a}^{2}+{b}^{2})$x2-2m${k}_{1}^{2}{a}^{3}$x+${m}^{2}{k}_{1}^{2}{a}^{4}$-a2b2=0,
由△=$(-2m{k}_{1}^{2}{a}^{3})^{2}$-4$({k}_{1}^{2}{a}^{2}+{b}^{2})$(${m}^{2}{k}_{1}^{2}{a}^{4}$-a2b2)=0,
化简得:${k}_{1}^{2}$=$\frac{{b}^{2}}{{a}^{2}}$$•\frac{1}{{m}^{2}-1}$,
同理可得${k}_{2}^{2}$=$\frac{{b}^{2}}{{a}^{2}}•({m}^{2}-1)$,
∴${k}_{1}^{2}{k}_{2}^{2}$=$\frac{{b}^{4}}{{a}^{4}}$=$(-\frac{1}{4})^{2}$=$\frac{1}{16}$,
因此$\frac{b}{a}$=$\frac{1}{2}$,∴椭圆的离心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{{\sqrt{3}}}{2}$.
故答案为:$\frac{{\sqrt{3}}}{2}$
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相切的充要条件、斜率计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 直角三角形 | ||
| C. | 等腰(非等边)三角形 | D. | 三边均不相等的三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 周期为$\frac{π}{4}$的偶函数 | B. | 周期为$\frac{π}{4}$的奇函数 | ||
| C. | 当x=$\frac{π}{4}$时,函数的最大值为4 | D. | 当x=$\frac{π}{4}$时,函数的最小值为2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{7}$ | B. | -7 | C. | $\frac{1}{7}$ | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 样本容量一定小于总体容量 | |
| B. | 用样本平均数去估计总体平均数时,估计的精确性与样本容量无关 | |
| C. | 一批产品,如果所测某种量的平均值与要求的标准值一致,则说明该产品在这方面是全部合格的 | |
| D. | 如果样本方差等于零,则总体方差也一定等于0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com