
分析 (Ⅰ)根据复合命题的真假得到p,q都为真,分别求出p,q为真时x的范围,即可求出答案.
(Ⅱ)化简p,根据命题的否定得到$A=({\frac{m-1}{2},\frac{m+1}{2}})$,$B=({-2,\frac{1}{3}})$,P是q的充分非必要条件,A是B的真子集,即求出m的范围.
解答 解:(Ⅰ)∵p∧q为真,∴p,q都为真…(1分)
又m=1,∴p真;|2x-1|≥1,即x≤0或x≥1…(2分)
$q真;\frac{1-3x}{x+2}>0$,∴(1-3x)(x+2)>0,即$-2<x<\frac{1}{3}$…(4分)
由$\left\{\begin{array}{l}x≤0或x≥1\\-2<x<\frac{1}{3}\end{array}\right.得-2<x≤0$,
∴实数x的取值范围为(-2,0]…(6分)
(Ⅱ)∵p:实数x满足|2x-m|≥1,∴?p;|2x-m|<1,即$\frac{m-1}{2}<x<\frac{m+1}{2}$
令$A=({\frac{m-1}{2},\frac{m+1}{2}})$…(7分)
$q;-2<x<\frac{1}{3}$,令$B=({-2,\frac{1}{3}})$…(8分)
∵?P是q的充分非必要条件,A是B的真子集…(9分)
∴$\left\{\begin{array}{l}\frac{m-1}{2}≥-2\\ \frac{m+1}{2}≤\frac{1}{3}\end{array}\right.(不能同时取等)$,得 $-3≤m≤-\frac{1}{3}$
∴实数m的取值范围是$[{-3,-\frac{1}{3}}]$…(12分)
点评 本题主要考查充分条件、必要条件、充要条件的定义,集合间的包含关系,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
如表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5海里 | B. | 5$\sqrt{2}$海里 | C. | 10海里 | D. | 10$\sqrt{2}$海里 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p∨q | B. | ¬p∧¬q | C. | p∧¬q | D. | p∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
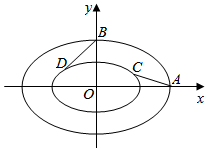 如图,内外两个椭圆的离心率相同,从外层椭圆顶点向内层椭圆引切线AC、BD,设内层椭圆方程$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),若直线AC与BD的斜率之积为-$\frac{1}{4}$,则椭圆的离心率为$\frac{{\sqrt{3}}}{2}$.
如图,内外两个椭圆的离心率相同,从外层椭圆顶点向内层椭圆引切线AC、BD,设内层椭圆方程$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),若直线AC与BD的斜率之积为-$\frac{1}{4}$,则椭圆的离心率为$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com