
分析 (1)设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),由题意可得c=1,即a2-b2=1,再由弦长$\frac{2{b}^{2}}{a}$=3,解方程可得a,b,进而得到椭圆方程;
(2)讨论若l1,l2中有一个的斜率不存在,另一条为0,易得$\frac{1}{|P{{\;}_{1}P}_{2}|}$+$\frac{1}{|{P}_{3}{P}_{4}|}$=$\frac{1}{4}$+$\frac{1}{3}$=$\frac{7}{12}$;若l1,l2的斜率都存在,且不为0,设l1:y=k(x+1),l2:y=-$\frac{1}{k}$(x+1),联立椭圆方程,运用韦达定理和弦长公式,计算即可得到定值;再由基本不等式,可得|P1P2|•|P3P4|≥($\frac{24}{7}$)2=$\frac{576}{49}$,由四边形的面积公式即可得到所求最小值.
解答 解:(1)设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
由题意可得c=1,即a2-b2=1,
令x=c,可得y=±b$\sqrt{1-\frac{{c}^{2}}{{a}^{2}}}$=±$\frac{{b}^{2}}{a}$,
即有$\frac{2{b}^{2}}{a}$=3,解得a=2,b=$\sqrt{3}$,
即有椭圆方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)证明:若l1,l2中有一个的斜率不存在,另一条为0,
此时$\frac{1}{|P{{\;}_{1}P}_{2}|}$+$\frac{1}{|{P}_{3}{P}_{4}|}$=$\frac{1}{4}$+$\frac{1}{3}$=$\frac{7}{12}$;
若l1,l2的斜率都存在,且不为0,设l1:y=k(x+1),l2:y=-$\frac{1}{k}$(x+1),
由$\left\{\begin{array}{l}{y=-\frac{1}{k}(x+1)}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$消去x,可得(4+3k2)y2+6ky-9=0,
设P3(x3,y3),P4(x4,y4),可得y3+y4=-$\frac{6k}{4+3{k}^{2}}$,y3y4=-$\frac{9}{4+3{k}^{2}}$,
|P3P4|=$\sqrt{1+{k}^{2}}$•$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$
=$\sqrt{1+{k}^{2}}$•$\sqrt{\frac{36{k}^{2}}{(4+3{k}^{2})^{2}}+\frac{36}{4+3{k}^{2}}}$=$\frac{12(1+{k}^{2})}{4+3{k}^{2}}$,
将k换为-$\frac{1}{k}$,可得|P1P2|=$\frac{12(1+{k}^{2})}{3+4{k}^{2}}$,
则$\frac{1}{|P{{\;}_{1}P}_{2}|}$+$\frac{1}{|{P}_{3}{P}_{4}|}$=$\frac{4+3{k}^{2}}{12(1+{k}^{2})}$+$\frac{3+4{k}^{2}}{12(1+{k}^{2})}$=$\frac{7(1+{k}^{2})}{12(1+{k}^{2})}$=$\frac{7}{12}$,
综上可得,$\frac{1}{|P{{\;}_{1}P}_{2}|}$+$\frac{1}{|{P}_{3}{P}_{4}|}$为定值$\frac{7}{12}$;
由$\frac{1}{|P{{\;}_{1}P}_{2}|}$+$\frac{1}{|{P}_{3}{P}_{4}|}$=$\frac{7}{12}$≥2$\sqrt{\frac{1}{|{P}_{1}{P}_{2}|•|{P}_{3}{P}_{4}|}}$,
则|P1P2|•|P3P4|≥($\frac{24}{7}$)2=$\frac{576}{49}$,
可得四边形P1P2P3P4面积S=$\frac{1}{2}$|P1P2|•|P3P4|≥$\frac{288}{49}$,
当且仅当|P1P2|=|P3P4|,即k=±1,面积取得最小值$\frac{288}{49}$.
点评 本题考查椭圆的方程的求法,注意运用垂直于对称轴的弦长,考查直线方程和椭圆方程,运用韦达定理和弦长公式,考查四边形面积的最值的求法,注意运用基本不等式,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | y=-cos4x | B. | y=-cosx | C. | y=sin(x+$\frac{π}{4}$) | D. | y=-sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
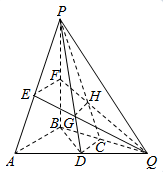 如图所示,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.
如图所示,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
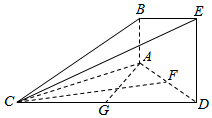 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD是等边三角形,AD=DE=2AB=2,F,G分别为AD,DC的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD是等边三角形,AD=DE=2AB=2,F,G分别为AD,DC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
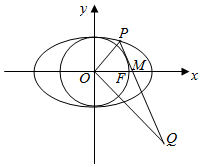 在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,右焦点F(1,0).
在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,右焦点F(1,0).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
如表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
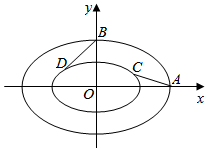 如图,内外两个椭圆的离心率相同,从外层椭圆顶点向内层椭圆引切线AC、BD,设内层椭圆方程$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),若直线AC与BD的斜率之积为-$\frac{1}{4}$,则椭圆的离心率为$\frac{{\sqrt{3}}}{2}$.
如图,内外两个椭圆的离心率相同,从外层椭圆顶点向内层椭圆引切线AC、BD,设内层椭圆方程$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),若直线AC与BD的斜率之积为-$\frac{1}{4}$,则椭圆的离心率为$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com