练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．下列说法正确的是（　　）
    A．样本容量一定小于总体容量
    B．用样本平均数去估计总体平均数时，估计的精确性与样本容量无关
    C．一批产品，如果所测某种量的平均值与要求的标准值一致，则说明该产品在这方面是全部合格的
    D．如果样本方差等于零，则总体方差也一定等于0

    分析 根据平均数、方差、总体、个体、样本、样本容量的定义判定即可．

    解答 解：A．∵样本是总体的一部分，∴样本容量一定小于总体容量，故A正确；
    B．∵用样本平均数去估计总体平均数时，样本容量越大估计的精确性越大，∴用样本平均数去估计总体平均数时，估计的精确性与样本容量无关，错误；
    C．如果所测某种量的平均值与要求的标准值一致，只是说明该产品在某方面是全部合格的，∴一批产品，如果所测某种量的平均值与要求的标准值一致，则说明该产品在这方面是全部合格的，错误；
    D．如果总体方差等于零，则样本方差不一定等于零，∴如果总体方差等于零，则样本方差也一定等于零，错误；
    故选A．

    点评 本题主要考查平均数、方差、总体、个体、样本、样本容量的定义以及他们之间的关系，熟悉并掌握定进行逐一判断即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

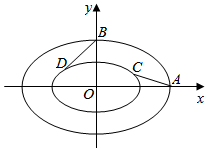    9．如图，内外两个椭圆的离心率相同，从外层椭圆顶点向内层椭圆引切线AC、BD，设内层椭圆方程$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0），若直线AC与BD的斜率之积为-$\frac{1}{4}$，则椭圆的离心率为$\frac{{\sqrt{3}}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．设f（x）是定义在R上的周期为3的函数，当x∈[-2，1）时，f（x）=$\left\{\begin{array}{l}4{x^2}-2，-2≤x≤0\\ x，0＜x＜1\end{array}$，则f（f（$\frac{21}{4}$））=（　　）
    A．-$\frac{3}{4}$B．$\frac{1}{4}$C．-$\frac{1}{4}$D．$\frac{3}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．解下列三角方程：
    （1）2sin2x+$\sqrt{3}$cosx+1=0．
    （2）3sin2x+8sinxcosx-3cos2x=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．若a∈R，试比较a2+1与4（a-1）的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．下列函数，图象关于原点对称的是（　　）
    A．f（x）=lgxB．f（x）=3xC．f（x）=lg（x+$\sqrt{1+{x}^{2}}$）D．f（x）=x2

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知回归直线的方程为$\widehat{y}$=2-2.5x，则x=25时，y的估计值是-60.5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

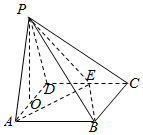    7．如图，在四棱锥P-ABCD中，等边△PAD所在的平面与正方形ABCD所在的平面互相垂直，O为AD的中点，E为DC的中点，且AD=2．
    （Ⅰ）求证：PO⊥平面ABCD；
    （Ⅱ）求二面角P-EB-A的余弦值；
    （Ⅲ）在线段AB上是否存在点M，使线段PM与△PAD所在平面成30°角．若存在，
    求出AM的长，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．为预防某种流感病毒爆发，某生物技术公司研制出一种新流感疫苗，为测试该疫苗的有效性（若疫苗有效的概率小于90%，则认为测试没有通过），公司选定2000个流感样本分成三组，测试结果如表：
     A组B组C组
    疫苗有效673xy
    疫苗无效7790Z
    已知在全体样本中随机抽取1个，抽到B组疫苗有效的概率是0.33．
    （1）求x的值；
    （2）现用分层抽样的方法在全体样本中抽取360个测试结果，问应在C组抽取多少个？

    查看答案和解析>>

    同步练习册答案