
| A组 | B组 | C组 | |
| 疫苗有效 | 673 | x | y |
| 疫苗无效 | 77 | 90 | Z |
分析 (1)根据抽样过程中每个个体被抽到的概率相等,列出方程即可求出x的值;
(II)求出每个个体被抽到的概率,利用这一组的总体个数乘以每个个体被抽到的概率,即得要求的结果数.
解答 解:(1)∵在全体样本中随机抽取1个,抽到B组疫苗有效的概率是0.33,
∴$\frac{x}{2000}$=0.33,
解得x=660;
(2)C组样本个数是
y+z=2000-(673+77+660+90)=500,
用分层抽样方法在全体中抽取360个测试结果,应在C组抽取的个数为
360×$\frac{500}{2000}$=90.
点评 本题考查了分层抽样方法以及在抽样过程中每个个体被抽到的概率相等的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | 样本容量一定小于总体容量 | |
| B. | 用样本平均数去估计总体平均数时,估计的精确性与样本容量无关 | |
| C. | 一批产品,如果所测某种量的平均值与要求的标准值一致,则说明该产品在这方面是全部合格的 | |
| D. | 如果样本方差等于零,则总体方差也一定等于0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3a,BC=2a,D是BC的中点,E,F分别是A1A,C1C上一点,且AE=CF=2a.
在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3a,BC=2a,D是BC的中点,E,F分别是A1A,C1C上一点,且AE=CF=2a.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
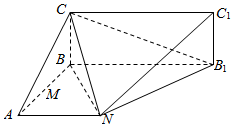 如图,AB⊥BB1,AN∥BB1,AB=BC=AN=$\frac{1}{2}$BB1=4,四边形BB1C1C为矩形,且平面BB1C1C⊥平面ABB1N.
如图,AB⊥BB1,AN∥BB1,AB=BC=AN=$\frac{1}{2}$BB1=4,四边形BB1C1C为矩形,且平面BB1C1C⊥平面ABB1N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120 | B. | 145 | C. | 150 | D. | 170 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com