
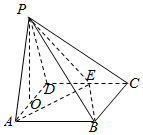
 如图,在四棱锥P-ABCD中,等边△PAD所在的平面与正方形ABCD所在的平面互相垂直,O为AD的中点,E为DC的中点,且AD=2.
如图,在四棱锥P-ABCD中,等边△PAD所在的平面与正方形ABCD所在的平面互相垂直,O为AD的中点,E为DC的中点,且AD=2.分析 (I)根据三线合一得出AO⊥AD,利用面面垂直的性质即可得出AO⊥平面ABCD;
(II)以O为原点建立空间直角坐标系,求出平面PBE和平面ABE的法向量,则两法向量夹角的余弦的绝对值为二面角的余弦值;
(III)假设存在符合条件的点M(1,x,0),求出平面PAD的法向量$\overrightarrow{OF}$,则|cos<$\overrightarrow{PM}$,$\overrightarrow{OF}$>|=$\frac{1}{2}$,解方程得出x,根据x的范围判断.
解答 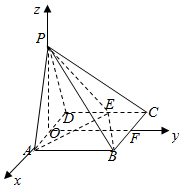 解:(Ⅰ)∵△PAD是等边三角形,O为AD的中点,
解:(Ⅰ)∵△PAD是等边三角形,O为AD的中点,
∴PO⊥AD,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PO?平面PAD,
∴PO⊥平面ABCD.
(Ⅱ)取BC的中点F,
∵底面ABCD是正方形,∴OF⊥AD,
∴PO,OF,AD两两垂直.
以O为原点,以OA、OF、OP为坐标轴建立空间直角坐标系如图:
则O(0,0,0),P(0,0,$\sqrt{3}$),B(1,2,0),E(-1,1,0),
∴$\overrightarrow{EP}$=(1,-1,$\sqrt{3}$),$\overrightarrow{EB}$=(2,1,0),$\overrightarrow{OP}$=(0,0,$\sqrt{3}$).
显然平面EBA的法向量为$\overrightarrow{OP}$=(0,0,$\sqrt{3}$).
设平面PBE的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EP}=0}\\{\overrightarrow{n}•\overrightarrow{EB}=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x-y+\sqrt{3}z=0}\\{2x+y=0}\end{array}\right.$,令x=1,得$\overrightarrow{n}$=(1,-2,-$\sqrt{3}$).
∴$\overrightarrow{n}•\overrightarrow{OP}$=-3,|$\overrightarrow{n}$|=2$\sqrt{2}$,|$\overrightarrow{OP}$|=$\sqrt{3}$,
∴cos<$\overrightarrow{n},\overrightarrow{OP}$>=-$\frac{\sqrt{6}}{4}$.
∵二面角P-EB-A为锐角,∴二面角P-EB-A的余弦值为$\frac{\sqrt{6}}{4}$.
(Ⅲ)设在线段AB上存在点M(1,x,0)(0<x≤2)使线段PM与平面PAD所在平面成30°角,
∵平面PAD的法向量为$\overrightarrow{OF}$=(0,2,0),$\overrightarrow{PM}$=(1,x,-$\sqrt{3}$),
∴cos<$\overrightarrow{OF}$,$\overrightarrow{PM}$>=$\frac{\overrightarrow{OF}•\overrightarrow{PM}}{|\overrightarrow{OF}||\overrightarrow{PM}|}$=$\frac{x}{\sqrt{4+{x}^{2}}}$.
∴sin30°=$\frac{x}{\sqrt{4+{x}^{2}}}$=$\frac{1}{2}$,解得$x=\frac{{2\sqrt{3}}}{3}$,符合题意.
∴在线段AB上存在点M,当线段$AM=\frac{{2\sqrt{3}}}{3}$时,PM与平面PAD所在平面成30°角.
点评 本题考查了线面垂直的判定,空间角的计算,空间向量的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{7}$ | B. | -7 | C. | $\frac{1}{7}$ | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 样本容量一定小于总体容量 | |
| B. | 用样本平均数去估计总体平均数时,估计的精确性与样本容量无关 | |
| C. | 一批产品,如果所测某种量的平均值与要求的标准值一致,则说明该产品在这方面是全部合格的 | |
| D. | 如果样本方差等于零,则总体方差也一定等于0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com