
分析 由θ得范围求得θ+$\frac{π}{4}$的范围,结合已知求得cos(θ+$\frac{π}{4}$),再由诱导公式求得sin($\frac{π}{4}-θ$)及cos($\frac{π}{4}-θ$),进一步由诱导公式及同角三角函数基本关系式求得tan(θ-$\frac{π}{4}$)的值.
解答 解:∵θ是第四象限角,
∴$-\frac{π}{2}+2kπ<θ<2kπ$,则$-\frac{π}{4}+2kπ<θ+\frac{π}{4}<\frac{π}{4}+2kπ,k∈Z$,
又sin(θ+$\frac{π}{4}$)=$\frac{3}{5}$,
∴cos(θ+$\frac{π}{4}$)=$\sqrt{1-si{n}^{2}(θ+\frac{π}{4})}=\sqrt{1-(\frac{3}{5})^{2}}=\frac{4}{5}$.
∴cos($\frac{π}{4}-θ$)=sin(θ+$\frac{π}{4}$)=$\frac{3}{5}$,sin($\frac{π}{4}-θ$)=cos(θ+$\frac{π}{4}$)=$\frac{4}{5}$.
则tan(θ-$\frac{π}{4}$)=-tan($\frac{π}{4}-θ$)=-$\frac{sin(\frac{π}{4}-θ)}{cos(\frac{π}{4}-θ)}$=$-\frac{\frac{4}{5}}{\frac{3}{5}}=-\frac{4}{3}$.
故答案为:-$\frac{4}{3}$.
点评 本题考查两角和与差的正切,考查诱导公式及同角三角函数基本关系式的应用,是基础题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
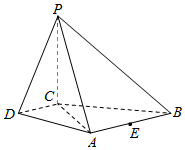 如图,在四棱锥P-ABCD中,PC⊥平面ABCD,AB∥DC,DC⊥AC.
如图,在四棱锥P-ABCD中,PC⊥平面ABCD,AB∥DC,DC⊥AC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 9 | C. | 10 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com