
分析 (Ⅰ)求出P,N,H的坐标,利用$\frac{{|{OH}|}}{{|{ON}|}}$=$\frac{|{y}_{H}|}{|{y}_{N}|}$,求$\frac{{|{OH}|}}{{|{ON}|}}$;
(Ⅱ)直线MH的方程为y=$\frac{p}{2t}$x+t,与抛物线方程联立,消去x可得y2-4ty+4t2=0,利用判别式可得结论.
解答 解:(Ⅰ)将直线l与抛物线方程联立,解得P($\frac{{t}^{2}}{2p}$,t),
∵M关于点P的对称点为N,
∴$\frac{{x}_{N}+{x}_{M}}{2}$=$\frac{{t}^{2}}{2p}$,$\frac{{y}_{N}+{y}_{M}}{2}$=t,
∴N($\frac{{t}^{2}}{p}$,t),
∴ON的方程为y=$\frac{p}{t}$x,
与抛物线方程联立,解得H($\frac{2{t}^{2}}{p}$,2t)
∴$\frac{{|{OH}|}}{{|{ON}|}}$=$\frac{|{y}_{H}|}{|{y}_{N}|}$=2;
(Ⅱ)由(Ⅰ)知kMH=$\frac{p}{2t}$,
∴直线MH的方程为y=$\frac{p}{2t}$x+t,与抛物线方程联立,消去x可得y2-4ty+4t2=0,
∴△=16t2-4×4t2=0,
∴直线MH与C除点H外没有其它公共点.
点评 本题考查直线与抛物线的位置关系,考查学生的计算能力,正确联立方程是关键.


科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{kπ}{2}$-$\frac{π}{6}$(k∈Z) | B. | x=$\frac{kπ}{2}$+$\frac{π}{6}$(k∈Z) | C. | x=$\frac{kπ}{2}$-$\frac{π}{12}$(k∈Z) | D. | x=$\frac{kπ}{2}$+$\frac{π}{12}$(k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (0,1) | C. | (-1,+∞) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sinx | B. | y=lnx | C. | y=ex | D. | y=x3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
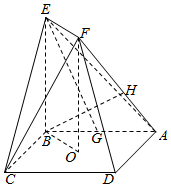 如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.
如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com