
分析 (Ⅰ)运用椭圆的离心率公式和三角形的面积公式,结合a,b,c的关系,解方程可得a=2,b=1,进而得到椭圆方程;
(Ⅱ)方法一、设椭圆上点P(x0,y0),可得x02+4y02=4,求出直线PA的方程,令x=0,求得y,|BM|;求出直线PB的方程,令y=0,可得x,|AN|,化简整理,即可得到|AN|•|BM|为定值4.
方法二、设P(2cosθ,sinθ),(0≤θ<2π),求出直线PA的方程,令x=0,求得y,|BM|;求出直线PB的方程,令y=0,可得x,|AN|,运用同角的平方关系,化简整理,即可得到|AN|•|BM|为定值4.
解答 解:(Ⅰ)由题意可得e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,
又△OAB的面积为1,可得$\frac{1}{2}$ab=1,
且a2-b2=c2,
解得a=2,b=1,c=$\sqrt{3}$,
可得椭圆C的方程为$\frac{{x}^{2}}{4}$+y2=1;
(Ⅱ)证法一:设椭圆上点P(x0,y0),
可得x02+4y02=4,
直线PA:y=$\frac{{y}_{0}}{{x}_{0}-2}$(x-2),令x=0,可得y=-$\frac{2{y}_{0}}{{x}_{0}-2}$,
则|BM|=|1+$\frac{2{y}_{0}}{{x}_{0}-2}$|;
直线PB:y=$\frac{{y}_{0}-1}{{x}_{0}}$x+1,令y=0,可得x=-$\frac{{x}_{0}}{{y}_{0}-1}$,
则|AN|=|2+$\frac{{x}_{0}}{{y}_{0}-1}$|.
可得|AN|•|BM|=|2+$\frac{{x}_{0}}{{y}_{0}-1}$|•|1+$\frac{2{y}_{0}}{{x}_{0}-2}$|
=|$\frac{({x}_{0}+2{y}_{0}-2)^{2}}{({x}_{0}-2)({y}_{0}-1)}$|=|$\frac{{{x}_{0}}^{2}+4{{y}_{0}}^{2}+4+4{x}_{0}{y}_{0}-4{x}_{0}-8{y}_{0}}{2+{x}_{0}{y}_{0}-{x}_{0}-2{y}_{0}}$|
=|$\frac{8+4{x}_{0}{y}_{0}-4{x}_{0}-8{y}_{0}}{2+{x}_{0}{y}_{0}-{x}_{0}-2{y}_{0}}$|=4,
即有|AN|•|BM|为定值4.
证法二:设P(2cosθ,sinθ),(0≤θ<2π),
直线PA:y=$\frac{sinθ}{2cosθ-2}$(x-2),令x=0,可得y=-$\frac{sinθ}{cosθ-1}$,
则|BM|=|$\frac{sinθ+cosθ-1}{1-cosθ}$|;
直线PB:y=$\frac{sinθ-1}{2cosθ}$x+1,令y=0,可得x=-$\frac{2cosθ}{sinθ-1}$,
则|AN|=|$\frac{2sinθ+2cosθ-2}{1-sinθ}$|.
即有|AN|•|BM|=|$\frac{2sinθ+2cosθ-2}{1-sinθ}$|•|$\frac{sinθ+cosθ-1}{1-cosθ}$|
=2|$\frac{si{n}^{2}θ+co{s}^{2}θ+1+2sinθcosθ-2sinθ-2cosθ}{1+sinθcosθ-sinθ-cosθ}$|
=2|$\frac{2+2sinθcosθ-2sinθ-2cosθ}{1+sinθcosθ-sinθ-cosθ}$|=4.
则|AN|•|BM|为定值4.
点评 本题考查椭圆的方程的求法,注意运用椭圆的离心率和基本量的关系,考查线段积的定值的求法,注意运用直线方程和点满足椭圆方程,考查化解在合理的运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{x}$-$\frac{1}{y}$>0 | B. | sinx-siny>0 | C. | ($\frac{1}{2}$)x-($\frac{1}{2}$)y<0 | D. | lnx+lny>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 立定跳远(单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
| 30秒跳绳(单位:次) | 63 | a | 75 | 60 | 63 | 72 | 70 | a-1 | b | 65 |
| A. | 2号学生进入30秒跳绳决赛 | B. | 5号学生进入30秒跳绳决赛 | ||
| C. | 8号学生进入30秒跳绳决赛 | D. | 9号学生进入30秒跳绳决赛 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
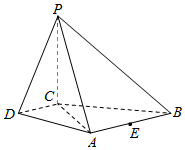 如图,在四棱锥P-ABCD中,PC⊥平面ABCD,AB∥DC,DC⊥AC.
如图,在四棱锥P-ABCD中,PC⊥平面ABCD,AB∥DC,DC⊥AC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com