
分析 根据“伴随点”的定义,分别进行判断即可,对应不成立的命题,利用特殊值法进行排除即可.
解答 解:①设A(0,1),则A的“伴随点”为A′(1,0),
而A′(1,0)的“伴随点”为(0,-1),不是A,故①错误,
②若点在单位圆上,则x2+y2=1,
即P(x,y)不是原点时,定义P的“伴随点”为P(y,-x),
满足y2+(-x)2=1,即P′也在单位圆上,故②正确,
③若两点关于x轴对称,设P(x,y),对称点为Q(x,-y),
则Q(x,-y)的“伴随点”为Q′(-$\frac{y}{{x}^{2}+{y}^{2}}$,$\frac{-x}{{x}^{2}+{y}^{2}}$),
则Q′(-$\frac{y}{{x}^{2}+{y}^{2}}$,$\frac{-x}{{x}^{2}+{y}^{2}}$)与P′($\frac{y}{{x}^{2}+{y}^{2}}$,$\frac{-x}{{x}^{2}+{y}^{2}}$)关于y轴对称,故③正确,
④∵(-1,1),(0,1),(1,1)三点在直线y=1上,
∴(-1,1)的“伴随点”为($\frac{1}{1+1}$,$\frac{1}{1+1}$),即($\frac{1}{2}$,$\frac{1}{2}$),
(0,1)的“伴随点”为(1,0),(1,1的“伴随点”为($\frac{1}{1+1}$,-$\frac{1}{1+1}$),即($\frac{1}{2}$,-$\frac{1}{2}$),
则($\frac{1}{2}$,$\frac{1}{2}$),(1,0),($\frac{1}{2}$,-$\frac{1}{2}$)三点不在同一直线上,故④错误,
故答案为:②③
点评 本题主要考查命题的真假判断,正确理解“伴随点”的定义是解决本题的关键.考查学生的推理能力.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sinx | B. | y=lnx | C. | y=ex | D. | y=x3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{43}{4}$ | B. | $\frac{49}{4}$ | C. | $\frac{37+6\sqrt{3}}{4}$ | D. | $\frac{37+2\sqrt{33}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
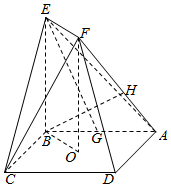 如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.
如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
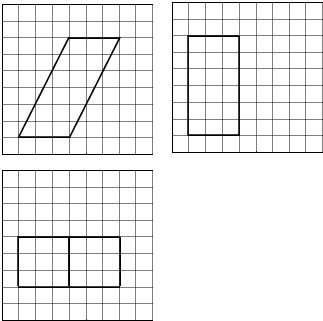
| A. | 18+36$\sqrt{5}$ | B. | 54+18$\sqrt{5}$ | C. | 90 | D. | 81 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com