
如图, 平面
平面 ,
, ,
,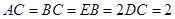 ,
, ,
, 分别为
分别为 的中点.
的中点.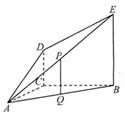
(I)证明: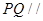 平面
平面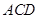 ;
;
(II)求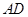 与平面
与平面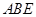 所成角的正弦值.
所成角的正弦值.
(I)只需证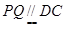 ;(II)
;(II)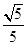 。
。
解析试题分析:(I)证明:连接 , 在
, 在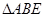 中,
中, 分别是
分别是 的中点,所以
的中点,所以 , 又
, 又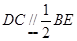 ,所以
,所以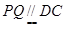 ,又
,又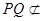 平面ACD ,DC
平面ACD ,DC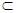 平面ACD, 所以
平面ACD, 所以 平面ACD。
平面ACD。
(Ⅱ)在 中,
中,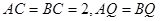 ,所以
,所以
而DC 平面ABC,
平面ABC,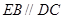 ,所以
,所以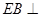 平面ABC
平面ABC
而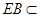 平面ABE, 所以平面ABE
平面ABE, 所以平面ABE 平面ABC, 所以
平面ABC, 所以 平面ABE
平面ABE
由(Ⅰ)知四边形DCQP是平行四边形,所以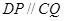
所以 平面ABE, 所以直线AD在平面ABE内的射影是AP,
平面ABE, 所以直线AD在平面ABE内的射影是AP,
所以直线AD与平面ABE所成角是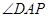
在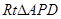 中,
中, ,
,
所以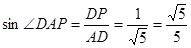 。
。
考点:线面平行的判定定理;线面角。
点评:本题主要考查了空间中直线与平面所成的角,属立体几何中的常考题型,较难.本题也可以用向量法来做。而对于利用向量法求线面角关键是正确写出点的坐标和求解平面的一个法向量。注意计算要仔细、认真。


科目:高中数学 来源: 题型:解答题
如图,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE,F为CD中点.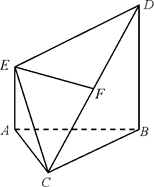
(Ⅰ)求证:EF⊥平面BCD;
(Ⅱ)求二面角C-DE-A的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=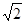 ,D为AA1中点,BD与AB1交于点O,CO丄侧面ABB1A1.
,D为AA1中点,BD与AB1交于点O,CO丄侧面ABB1A1.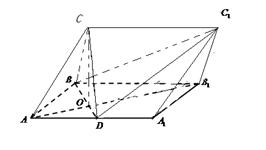
(Ⅰ)证明:BC丄AB1;
(Ⅱ)若OC=OA,求二面角C1-BD-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.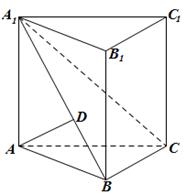
(1)求证:平面A1BC⊥平面ABB1A1;
(2)若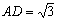 ,AB=BC=2,P为AC中点,求三棱锥
,AB=BC=2,P为AC中点,求三棱锥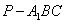 的体积。
的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知菱形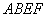 所在平面与直角梯形
所在平面与直角梯形 所在平面互相垂直,
所在平面互相垂直,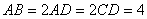 ,
,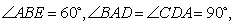 点
点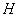 ,
,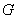 分别是线段
分别是线段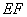 ,
, 的中点.
的中点. 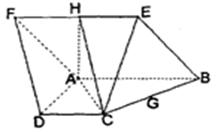
(I)求证:平面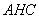
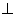 平面
平面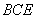 ;
;
(Ⅱ)点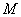 在直线
在直线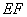 上,且
上,且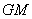 //平面
//平面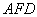 ,求平面
,求平面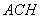 与平面
与平面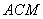 所成角的余弦值。
所成角的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C、D的点,AE=3,正方形ABCD的边长为 .
.
(1)求证:平面ABCD丄平面ADE;
(2)求四面体BADE的体积;
(3)试判断直线OB是否与平面CDE垂直,并请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四边形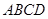 中,
中,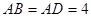 ,
,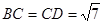 ,点
,点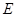 为线段
为线段 上的一点.现将
上的一点.现将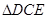 沿线段
沿线段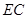 翻折到
翻折到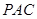 (点
(点 与点
与点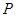 重合),使得平面
重合),使得平面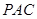
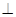 平面
平面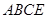 ,连接
,连接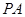 ,
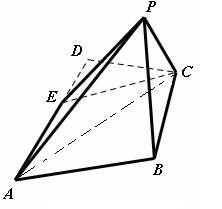
,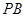 .
.
(Ⅰ)证明: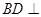 平面
平面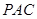 ;
;
(Ⅱ)若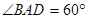 ,且点
,且点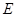 为线段
为线段 的中点,求二面角
的中点,求二面角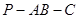 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com