
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
分析 由已知向量的坐标可得$\overrightarrow{a}⊥\overrightarrow{b}$,从而得到向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{2}$.
解答 解:∵$\overrightarrow{a}=(\sqrt{3},1)$,$\overrightarrow{b}=(-1,\sqrt{3})$,
∴$\overrightarrow{a}•\overrightarrow{b}$=$(\sqrt{3},1)•(-1,\sqrt{3})=0$,
∴$\overrightarrow{a}⊥\overrightarrow{b}$,
则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ为$\frac{π}{2}$.
故选:D.
点评 本题考查平面向量的数量积运算,考查了向量垂直的坐标表示,是基础题.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:解答题
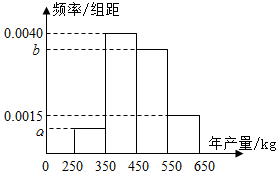 某人租用一块土地种植一种瓜类作物,租期5年,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg时,单位售价为10元/kg.
某人租用一块土地种植一种瓜类作物,租期5年,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg时,单位售价为10元/kg.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | $\frac{5}{4}$ | D. | -$\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com