【题目】为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：
喜爱打篮球 | 不喜爱打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为
．
（1）请将上面的列联表补充完整；
（2）是否有99%的把握认为“喜爱打篮球与性别有关”？说明你的理由．
参考公式：独立性检测中，随机变量
，
其中
为样本容量
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
小学教材完全解读系列答案科目：高中数学 来源： 题型：
【题目】△ABC的内角A，B，C所对应的边分别为a，b，c．
（Ⅰ）若a，b，c成等差数列，证明：sinA+sinC=2sin（A+C）；
（Ⅱ）若a，b，c成等比数列，求cosB的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列命题中的说法正确的是（ ）
A. 若向量
，则存在唯一的实数
使得
；
B. 命题“若
，则
”的否命题为“若，则
”；
C. 命题“
，使得
”的否定是：“
，均有
”；
D. 命题“在
中，
是
的充要条件”的逆否命题为真命题.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某市为了考核甲，乙两部门的工作情况，随机访问了50位市民，根据这50位市民对这两部门的评分（评分越高表明市民的评价越高），绘制茎叶图如下：
（1）分别估计该市的市民对甲，乙两部门评分的中位数；
（2）分别估计该市的市民对甲，乙两部门的评分高于90的概率；
（3）根据茎叶图分析该市的市民对甲，乙两部门的评价．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某少数民族的刺绣有着悠久的历史，如图4①，②，③，④为她们刺绣最简单的四个图案，这些图案都是由小正方形构成，小正方形数越多刺绣越漂亮．现按同样的规律刺绣(小正方形的摆放规律相同)，设第n个图形包含f(n)个小正方形．
(1)求出f(5)的值；
(2)利用合情推理的“归纳推理思想”，归纳出f(n＋1)与f(n)之间的关系式，并根据你得到的关系式求出f(n)的表达式；
(3)求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，某地村庄P与村庄O的距离为
千米，从村庄O出发有两条道路
，经测量，的夹角为
，OP与
的夹角
满足
（其中
），现要经过P修一条直路分别与道路交汇于
两点，并在处设立公共设施．
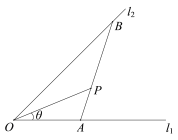
（1）已知修建道路
的单位造价分别为2m元/千米和m元/千米，若两段道路的总造价相等，求此时点之间的距离；
（2）考虑环境因素，需要对
段道路进行翻修，段的翻修单价分别为n元/千米和
元/千米，要使两段道路的翻修总价最少，试确定点的位置．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在正方体
中，
，
，
分别是
，
，
的中点．
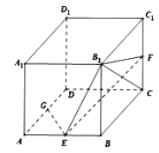
（1）求异面直线
与
所成角的大小；
（2）棱
上是否存在点
，使
平面
？若存在，求出
的值；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列命题中，正确的为________（正确序号全部填上）
（1）空间中，一个角的两边与另一个角的两边分别平行，则这两个角相等或互补；
（2）一个二面角的两个半平面与另一个二面角的两个半平面分别垂直，则这两个二面角相等或互补；
（3）直线
，
为异面直线，所成角的大小为
，过空间一点
作直线
，使l与直线及直线都成相等的角
，这样的直线可作3条；
（4）直线与平面
相交，过直线可作唯一的平面与平面垂直．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
