
分析 (1)设T(x,y),则$\frac{y}{x+2}•\frac{y}{x-2}=-λ$,由此能求出曲线C的方程及其焦点坐标.
(2)椭圆长轴端点到同侧焦点的距离是椭圆上的点到焦点的最近距离,从而2-2$\sqrt{1-λ}$=1,进而求出曲线C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.直线y=k(x-1)交x轴于Q(1,0),联立$\left\{\begin{array}{l}{y=k(x-1)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得(4k2+3)x2-8k2x+4k2-12=0,由此利用韦达定理、直线方程,结合已知条件能证明k•k′为定值.
解答 解:(1)设T(x,y),则$\frac{y}{x+2}•\frac{y}{x-2}=-λ$,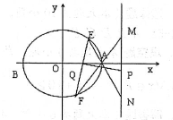
整理,得:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{4λ}=1$(x≠±2),
又A(2,0)、B(-2,0)也符合上式,
∴曲线C:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{4λ}$=1,(λ>0,λ≠1),
当0<λ<1时,曲线C是焦点在x轴上的椭圆,焦点为(-2$\sqrt{1-λ}$,0),(2$\sqrt{1-λ}$,0),
当λ>1时,曲线C是焦点在y轴上的椭圆,焦点为(0,-2$\sqrt{λ-1}$),(0,$2\sqrt{λ-1}$).
(2)∵0<λ<1,曲线C是焦点在y轴上的椭圆,其焦点为(-2$\sqrt{1-λ}$,0),(2$\sqrt{1-λ}$,0),
椭圆长轴端点到同侧焦点的距离是椭圆上的点到焦点的最近距离,
曲线C上的点到其焦点的最近距离为1.
∴2-2$\sqrt{1-λ}$=1,解得$λ=\frac{3}{4}$,
∴曲线C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
直线y=k(x-1)交x轴于Q(1,0),
设E(x1,y1),F(x2,y2),
联立$\left\{\begin{array}{l}{y=k(x-1)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得(4k2+3)x2-8k2x+4k2-12=0,
∴${x}_{1}+{x}_{2}=\frac{8{k}^{2}}{4{k}^{2}+3}$,x1x2=$\frac{4{k}^{2}-12}{4{k}^{2}+3}$,①
直线AE方程为y=$\frac{{y}_{1}}{{x}_{1}-2}(x-2)$,交直线x=3于点N(3,$\frac{{y}_{1}}{{x}_{1}-2}$),
直线AF方程为y=$\frac{{y}_{2}}{{x}_{2}-2}(x-2)$,交直线x=3于点M(3,$\frac{{y}_{2}}{{x}_{2}-2}$),
∴线段MN的中点P(3,$\frac{1}{2}(\frac{{y}_{1}}{{x}_{1}-2}+\frac{{y}_{2}}{{x}_{2}-2})$),
∴直线PQ的斜率为:
k′=$\frac{\frac{1}{2}(\frac{{y}_{1}}{{x}_{1}-2}+\frac{{y}_{2}}{{x}_{2}-2})}{3-1}$=$\frac{{y}_{1}{x}_{2}+{y}_{2}{x}_{1}-2({y}_{1}+{y}_{2})}{4[{x}_{1}{x}_{2}-2({x}_{1}+{x}_{2})+4]}$=$\frac{2k{x}_{1}{x}_{2}-3k({x}_{1}+{x}_{2})+4k}{4[{x}_{1}{x}_{2}-2({x}_{1}+{x}_{2})+41]}$,②
将①代入②,整理,得${k}^{'}=-\frac{3}{4k}$,
∴kk′=-$\frac{3}{4}$,
∴k•k′为定值-$\frac{3}{4}$.
点评 本题考查曲线方程及焦点坐标的求法,考查两直线的斜率之积为定值的证明,是中档题,解题时要认真审题,注意椭圆性质、韦达定理、直线方程的性质的合理运用.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:解答题
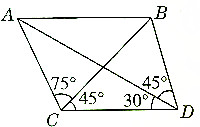 如图,在四边形ABDC中,CD=$\sqrt{3}$,∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,求AB的长.
如图,在四边形ABDC中,CD=$\sqrt{3}$,∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,求AB的长.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
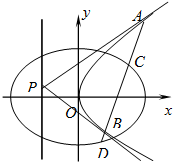 已知中心在原点的椭圆Γ1和抛物线Γ2有相同的焦点(1,0),椭圆Γ1的离心率为$\frac{1}{2}$,抛物线Γ2的顶点为原点.
已知中心在原点的椭圆Γ1和抛物线Γ2有相同的焦点(1,0),椭圆Γ1的离心率为$\frac{1}{2}$,抛物线Γ2的顶点为原点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{5}+\frac{2}{5}i$ | B. | $\frac{1}{5}-\frac{2}{5}i$ | C. | $-\frac{1}{5}-\frac{2}{5}i$ | D. | $\frac{1}{5}+\frac{2}{5}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
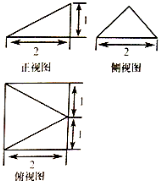
| A. | 4 | B. | $\frac{4}{3}$ | C. | 7+$\sqrt{5}$ | D. | 5+2$\sqrt{2}$+$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com