练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．已知曲线C1的方程为x2+y2=1，过平面上一点P1作C1的两条切线，切点分别为A1、B1，且满足∠A1P1B1=$\frac{π}{3}$，记P1的轨迹为C2，过一点P2作C2的两条切线，切点分别为A2，B2满足∠A2P2B2=$\frac{π}{3}$，记P2的轨迹为C3，按上述规律一直进行下去…，记an=|AnAn+1|max且Sn为数列{$\frac{1}{{a}_{n}}$}的前n项和，则满足|Sn-$\frac{2}{3}$|＜$\frac{1}{100}$的最小的n是（　　）
    A．5B．6C．7D．8

    分析 设P1（x，y），则|OP1|=2|OA1|=2，可得方程C2：x2+y2=4．同理可得P2的方程C3为：x2+y2=16．设A1（cosθ，sinθ），A2（2cosα，2sinα），可得|A1A2|=$\sqrt{5-4cos（α-θ）}≤3=1+2$，同理可得：an=|AnAn+1|max=2n-1+2n．可得$\frac{1}{{a}_{n}}=\frac{1}{3•{2}^{n-1}}$．可得数列{$\frac{1}{{a}_{n}}$}的前n项和Sn，代入|Sn-$\frac{2}{3}$|=$\frac{1}{3•{2}^{n-1}}$＜$\frac{1}{100}$，由此能求出n．

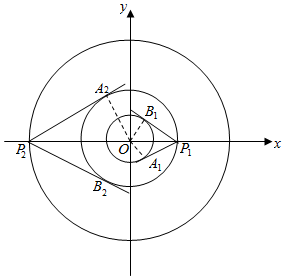    解答 解：设P1（x，y），则|OP1|=2|OA1|=2，
    可得方程C2：x2+y2=4．
    同理可得P2的方程C3为：x2+y2=16．
    设A1（cosθ，sinθ），A2（2cosα，2sinα）
    |A1A2|=$\sqrt{（cosθ-2cosα）^{2}+（sinθ-2sinα）^{2}}$
    =$\sqrt{5-4cos（α-θ）}$≤3=1+2，
    同理可得：an=|AnAn+1|max=2n-1+2n．
    $\frac{1}{{a}_{n}}$=$\frac{1}{{2}^{n-1}+{2}^{n}}$=$\frac{1}{3•{2}^{n-1}}$．
    数列{$\frac{1}{{a}_{n}}$}的前n项和Sn=$\frac{1}{3}$×$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$=$\frac{1}{3}（1-\frac{1}{{2}^{n}}）$，
    则满足|Sn-$\frac{2}{3}$|=$\frac{1}{3•{2}^{n-1}}$＜$\frac{1}{100}$，解得n≥7．
    故选：C．

    点评 本题考查等比数列的通项公式与求和公式，考查数列递推公式、两点间距离公式、直线与圆相切的性质、勾股定理等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    5．若关于x的方程x2-mx+m=0没有实数根，则实数m的取值范围是（0，4）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知数列{an}满足：a1=1，$\frac{1}{{{a_{n+1}}}}=\frac{{{a_n}+1}}{a_n}$（n∈N*），则数列{an}的通项公式为（　　）
    A．${a_n}=\frac{1}{n}$B．${a_n}=\frac{1}{n-1}$C．${a_n}=\frac{n}{n+1}$D．${a_n}=\frac{1}{n+1}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知直线l1过点A（2，1），直线l2：2x-y-1=0．
    （Ⅰ）若直线l1与直线l2平行，求直线l1的方程；
    （Ⅱ）若直线l1与y轴、直线l2分别交于点M，N，|MN|=|AN|，求直线l1的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．把下列各角度化成弧度：
    （1）36°；（2）-150°；（3）1095°；（4）1440°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知正项数列{an}与正项数列{bn}的前n项和分别为An和Bn，且对任意n∈N*，an+1-an=2（bn+1-bn）恒成立．
    （1）若An=$\frac{1}{2}$（an-1）（an+2），n∈N*，求数列{an}的通项公式；
    （2）在（1）的条件下，若b1=1，求Bn；
    （3）若对任意n∈N*，恒有an=Bn及$\frac{{b}_{2}}{{a}_{1}{a}_{2}}$+$\frac{{b}_{3}}{{a}_{2}{a}_{3}}$+$\frac{{b}_{4}}{{a}_{3}{a}_{4}}$+…+$\frac{{b}_{n+1}}{{a}_{n}{a}_{n+1}}$＜$\frac{1}{3}$成立，求实数b1的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．设a=3x2-x+2，b=2x2+x-1，则a与b的大小关系为（　　）
    A．a＞bB．a=bC．a＜bD．与x有关

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．设m=3${∫}_{-1}^{1}$（x2+sinx）dx，则多项式（x+$\frac{1}{m\sqrt{x}}$）6的常数项（　　）
    A．-$\frac{5}{4}$B．$\frac{5}{4}$C．$\frac{20}{3}$D．$\frac{15}{16}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．设$\overrightarrow{e_1}，\overrightarrow{e_2}$是两个不共线的向量，已知$\overrightarrow{AB}=2\overrightarrow{e_1}+m\overrightarrow{e_2}，\overrightarrow{BC}=\overrightarrow{e_1}+3\overrightarrow{e_2}$，若A，B，C三点共线，则实数m=6．

    查看答案和解析>>

    同步练习册答案