Question

19．已知函数f（x）=x²-ax-4（a∈R）的两个零点为x₁，x₂，设x₁＜x₂．
（1）当a＞0时，证明：-2＜x₁＜0；
（2）若函数g（x）=x²-|f（x）|在区间（-∞，-2）和（2，+∞）上均单调递增，求a的取值范围．

Answer 1

分析 （1）使用求根公式解出x₁，利用a的范围和不等式的性质得出；
（2）求出g′（x），令g′（x）＞0，结合函数图象讨论a的范围，

解答 解：（1）令f（x）=0解得x₁=$\frac{a-\sqrt{{a}^{2}+16}}{2}$，x₂=$\frac{a+\sqrt{{a}^{2}+16}}{2}$．
∵$\sqrt{{a}^{2}+16}$＞$\sqrt{{a}^{2}}$=a，∴$\frac{a-\sqrt{{a}^{2}+16}}{2}$＜0．∵a＞0，∴$\sqrt{{a}^{2}+16}$＜$\sqrt{{a}^{2}+8a+16}$=a+4，∴$\frac{a-\sqrt{{a}^{2}+16}}{2}$＞$\frac{a-（a+4）}{2}$=-2．
∴-2＜x₁＜0．
（2）g（x）=x²-|x²-ax-4|，∴g′（x）=2x-|2x-a|，
∵g（x）在区间（-∞，-2）和（2，+∞）上均单调递增，∴g′（x）＞0，即2x＞|2x-a|，（x＞2）．
当a=0时，显然不成立，
若a＞0，作出y=2x和y=|2x-a|的函数图象如图：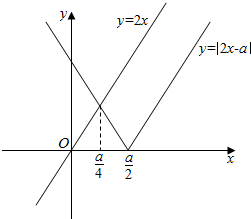

∴0＜$\frac{a}{4}≤2$，解得0＜a≤8．
若a＜0，作出y=2x和y=|2x-a|的函数图象如图：

有图象可知2x＜|2x-a|，故g′（x）＞0不成立，不符合题意．
综上，a的取值范围是（0，8]．

点评 本题主要考查二次函数的性质，导数与函数的单调性间的关系，体现了分类讨论、数形结合的、转化的数学思想，属于中档题．