
分析 (Ⅰ)由已知数列递推式可得,当n≥2时,an=Sn-Sn-1,整理可得an-1,则数列{an}的通项公式可求;
(Ⅱ)由(Ⅰ)可得Sn,代入cn=<$\frac{{{a_n}{a_{n+1}}}}{S_n}$>,利用裂项相消法求得数列{cn}的前n项和Tn.
解答 解:(Ⅰ)∵${S_n}={a_n}+{n^2}-1({n∈{N^*}})$,
当n≥2时,${a}_{n}={S}_{n}-{S}_{n-1}={a}_{n}+{n}^{2}-1-[{a}_{n-1}+(n-1)^{2}-1]$,
整理得:an-1=2n-1,
∴an=2n+1;
(Ⅱ)由(Ⅰ)知,${S}_{n}={n}^{2}+2n$,
∴$\frac{{a}_{n}{a}_{n+1}}{{S}_{n}}=\frac{(2n+1)(2n+3)}{{n}^{2}+2n}$=$\frac{4{n}^{2}+8n+3}{{n}^{2}+2n}=4+\frac{3}{{n}^{2}+2n}$.
∴当n=1时,c1=<4+1>=0,
当n≥2时,有0<$\frac{3}{{n}^{2}+2n}$<1.
∴${c}_{n}=\frac{3}{{n}^{2}+2n}=\frac{3}{2}(\frac{1}{n}-\frac{1}{n+2})$(n≥2).
∴Tn=c1+c2+…+cn
=0+$\frac{3}{2}(\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{5}+\frac{1}{4}-\frac{1}{6}+…+\frac{1}{n-1}-\frac{1}{n+1}+\frac{1}{n}-\frac{1}{n+2})$
=$\frac{3}{2}(\frac{1}{2}+\frac{1}{3}-\frac{1}{n+1}-\frac{1}{n+2})$=$\frac{5{n}^{2}+3n-8}{4{n}^{2}+12n+8}$.
验证n=1成立,
∴${T}_{n}=\frac{5{n}^{2}+3n-8}{4{n}^{2}+12n+8}$.
点评 本题考查数列求和,着重训练了裂项相消法,属中档题.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
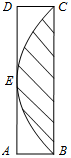 如图所示矩形ABCD边长AB=1,AD=4,抛物线顶点为边AD的中点E,且B,C两点在抛物线上,则从矩形内任取一点落在抛物线与边BC围成的封闭区域(包含边界上的点)内的概率是$\frac{2}{3}$.
如图所示矩形ABCD边长AB=1,AD=4,抛物线顶点为边AD的中点E,且B,C两点在抛物线上,则从矩形内任取一点落在抛物线与边BC围成的封闭区域(包含边界上的点)内的概率是$\frac{2}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,5} | B. | {x|x2≤1} | C. | (1,2) | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4) | B. | (4,+∞) | C. | (-∞,4)∪(4,+∞) | D. | (-∞,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,2) | B. | [-1,1] | C. | (0,1] | D. | (-∞,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com