
分析 由减函数可知f(x)在两段上均为减函数,且在第一段的最小值大于或等于第二段上的最大值,根据交点个数判断3a与2的大小关系,列出不等式组解出.
解答 解:∵f(x)是R上的单调递减函数,
∴y=x2+(2-4a)x+3a在(-∞,0)上单调递减,y=loga(x+1)在(0,+∞)上单调递减,
且f(x)在(-∞,0)上的最小值大于或等于f(0).
∴$\left\{\begin{array}{l}{2a-1≥0}\\{0<a<1}\\{3a≥0}\end{array}\right.$,解得$\frac{1}{2}$≤a≤1.
∵方程|f(x)|=2有两个不相等的实数根,
∴3a≤2,即a≤$\frac{2}{3}$.
综上,$\frac{1}{2}$≤a≤$\frac{2}{3}$.
故答案为[$\frac{1}{2}$,$\frac{2}{3}$].
点评 本题考查了分段函数的单调性,函数零点的个数判断,判断端点值的大小是关键,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | a>b>c | C. | c>a>b | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
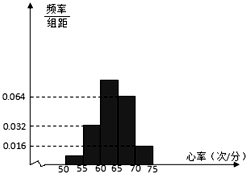 某高校要了解在校学生的身体健康状况,随机抽取了50名学生进行心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60)…第五组[70,75],按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.
某高校要了解在校学生的身体健康状况,随机抽取了50名学生进行心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60)…第五组[70,75],按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com