
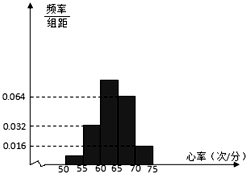
 某高校要了解在校学生的身体健康状况,随机抽取了50名学生进行心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60)…第五组[70,75],按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.
某高校要了解在校学生的身体健康状况,随机抽取了50名学生进行心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60)…第五组[70,75],按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.分析 (1)求出各组的频数,即可求a的值.
(2)若从第一、第五组两组数据中随机抽取两名学生的心率,确定基本事件的个数,即可求这两个心率之差的绝对值大于5的概率.
解答 解:(1)因为第二组数据的频率为 0.032×5=0.16,故第二组的频数为0.16×50=8,
第一组的频数为2a,第三组的频数为20,第四组的频数为16,第五组的频数为4
所以 2a=50-20-16-8-4=2⇒a=1.…(6分)
(2)第一组的数据有2个,第五组的数据有4个,故总的基本事件有15个,
符合题意的基本事件有8个,
所以这两个心率之差的绝对值大于5的概率$P=\frac{8}{15}$.…(12分)
点评 本题考查频率分布直方图,考查概率的计算,属于中档题.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4) | B. | (4,+∞) | C. | (-∞,4)∪(4,+∞) | D. | (-∞,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
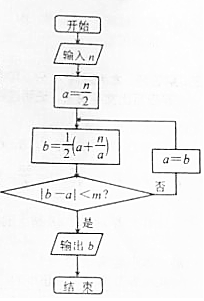 一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n为6时,输出结果为2.45,则m可以是( )
一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n为6时,输出结果为2.45,则m可以是( )| A. | 0.6 | B. | 0.1 | C. | 0.01 | D. | 0.05 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com