
分析 (Ⅰ)去掉绝对值符号,然后求解不等式即可解不等式f(x)>5;
(Ⅱ)利用绝对值的几何意义,求出f(x)的最小值,利用恒成立,转化不等式求解即可.
解答 (本小题满分10分)
解:(Ⅰ)原不等式可化为:$\left\{\begin{array}{l}x≤-1\\ 1-2x>5\end{array}\right.$或$\left\{\begin{array}{l}-1<x≤2\\ 3>5\end{array}\right.$或$\left\{\begin{array}{l}x>2\\ 2x-1>5.\end{array}\right.$…(3分)
解得:x<-2或x>3,
所以解集为:(-∞,-2)∪(3,+∞). …(5分)
(Ⅱ)因为|x-2|+|x+1|≥|x-2-(x+1)|=3,…(7分)
所以 f(x)≥3,当x≤-1时等号成立. 所以f(x)min=3.
又${({log_2}a)^2}-{log_{\sqrt{2}}}a≤3?{({log_2}a)^2}-2{log_2}a-3≤0?-1≤{log_2}a≤3$,
故$\frac{1}{2}≤a≤8$. …(10分)
点评 本题考查函数的恒成立,函数的最值的求法,绝对值不等式的几何意义的应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
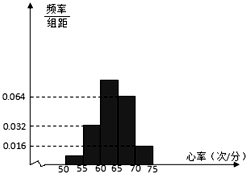 某高校要了解在校学生的身体健康状况,随机抽取了50名学生进行心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60)…第五组[70,75],按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.
某高校要了解在校学生的身体健康状况,随机抽取了50名学生进行心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60)…第五组[70,75],按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -8 | B. | -4 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (¬p)∧q | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 坐标系与参数方程 | 不等式选讲 | |||
| 人数及均分 | 人数 | 均分 | 人数 | 均分 |
| 男同学 | 14 | 8 | 6 | 7 |
| 女同学 | 8 | 6.5 | 12 | 5.5 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈(0,π),sinx=tanx | |
| B. | “?x∈R,x2+x+1>0”的否定是“?x0∈R,x02+x0+1<0” | |
| C. | ?θ∈R,函数f(x)=sin(2x+θ)都不是偶函数 | |
| D. | 条件p:$\left\{\begin{array}{l}{x+y>4}\\{xy>4}\end{array}\right.$,条件q:$\left\{\begin{array}{l}{x>2}\\{y>2}\end{array}\right.$则p是q的必要不充分条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com