
分析 (Ⅰ)由椭圆的焦距为2,离心率e为$\frac{1}{2}$.求出a,b,由此能求出椭圆的标准方程.
(Ⅱ)由题意,得O、M、P、n四点共圆,该圆的方程为(x-$\frac{1}{4}$)2+(y-$\frac{1}{2}$)2=$\frac{5}{16}$,圆O的方程为x2+y2=$\frac{1}{2}$,直线MN的方程为x+2y-1=0,设A(x1,y1),B(x2,y2),则${S}_{△ABG}=\frac{1}{2}$|GF||y1-y2|=|y1-y2|,从而S△ABG最大,|y1-y2|就最大.可设直线l的方程为x=my+1,由$\left\{\begin{array}{l}{x=my+1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得(3m2+4)y2+6my-9=0,由此利用根的判别式、韦达定理、弦长公式,能求出△ABG的面积的最大值.
解答 解:(Ⅰ)∵椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,焦距为2,离心率e为$\frac{1}{2}$.
∴由题意,2c=2,解得c=1,
由e=$\frac{c}{a}=\frac{1}{2}$,解得a=2.∴b=$\sqrt{4-1}=\sqrt{3}$.
∴椭圆的标准方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
(Ⅱ)由题意,得O、M、P、n四点共圆,
该圆的方程为(x-$\frac{1}{4}$)2+(y-$\frac{1}{2}$)2=$\frac{5}{16}$,
又圆O的方程为x2+y2=$\frac{1}{2}$,
∴直线MN的方程为x+2y-1=0,令y=0,得x=1,
即点F的坐标为(1,0),则点F关于y轴的对称点为G(-1,0).
设A(x1,y1),B(x2,y2),则${S}_{△ABG}=\frac{1}{2}$|GF||y1-y2|=|y1-y2|,
∴S△ABG最大,|y1-y2|就最大.
由题意知,直线l的斜率不为零,可设直线l的方程为x=my+1,
由$\left\{\begin{array}{l}{x=my+1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得(3m2+4)y2+6my-9=0,
∴${y}_{1}+{y}_{2}=\frac{-6m}{3{m}^{2}+4}$,${y}_{1}{y}_{2}=\frac{-9}{3{m}^{2}+4}$.
又∵直线l与椭圆C交于不同的两点,
∴△>0,即(6m)2+36(3m2+4)>0,m∈R,
则S△GAB=$\frac{1}{2}$|GF||y1-y2|=|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{12\sqrt{{m}^{2}+1}}{3{m}^{2}+4}$,
令t=$\sqrt{{m}^{2}+1}$,则t≥1,S△GAB=$\frac{12\sqrt{{m}^{2}+1}}{3{m}^{2}+4}$=$\frac{12t}{3{t}^{2}+1}$=$\frac{4}{t+\frac{\frac{1}{3}}{t}}$.
令f(t)=t+$\frac{\frac{1}{3}}{t}$,则函数f(t)在[$\frac{\sqrt{3}}{3}$,+∞)上单调递增,即当t≥1时,f(t)在[1,+∞)上单调递增,
∴f(t)≥f(1)=$\frac{4}{3}$,∴S△GAB≤3.
故△ABG的面积的最大值为3.
点评 本题考查椭圆方程的求法,考查三角形面积的最大值的求法,是中档题,解题时要认真审题,注意椭圆、直线方程、根的判别式、韦达定理、弦长公式等知识点的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若l∥α,l⊥m,则m⊥α | B. | 若l∥α,l⊥m,m?β,则α⊥β | ||
| C. | 若l∥α,l∥m,则m∥α | D. | 若α∥β,l∥α,l∥m,m?β,则m∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
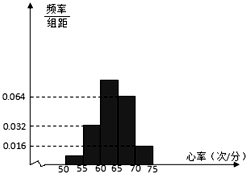 某高校要了解在校学生的身体健康状况,随机抽取了50名学生进行心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60)…第五组[70,75],按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.
某高校要了解在校学生的身体健康状况,随机抽取了50名学生进行心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60)…第五组[70,75],按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (¬p)∧q | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com