
分析 利用特征值与特征向量的定义,建立方程,求出a,b,即可求矩阵A,设l上点P(x,y)在A的作用下得到直线l′上一点P′(x′,y′),进一步求得x′,y′与x,y的关系,代入直线方程得答案.
解答 解:由题意,$[\begin{array}{l}{a}&{2}\\{b}&{4}\end{array}]$$[\begin{array}{l}{1}\\{1}\end{array}]$=3$[\begin{array}{l}{1}\\{1}\end{array}]$,∴$\left\{\begin{array}{l}{a+2=3}\\{b+4=3}\end{array}\right.$,
∴a=1,b=-1,
∴A=$[\begin{array}{l}{1}&{2}\\{-1}&{4}\end{array}]$,
设l上点P(x,y)在A的作用下得到直线l′上一点P′(x′,y′),
则$\left\{\begin{array}{l}{x′=x+2y}\\{y′=-x+4y}\end{array}\right.$,∴x=$\frac{1}{3}$(2x′-y′),y=$\frac{1}{6}$(x′+y′),
代入直线l的方程,化简得7x′-5y′-18=0,
即直线l′的方程为7x-5y-18=0.
点评 本题主要考查矩阵与变换、曲线在矩阵变换下的曲线的方程,考查运算求解能力及化归与转化思想,是基础题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0] | B. | [0,3) | C. | (3,4] | D. | (-1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
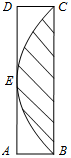 如图所示矩形ABCD边长AB=1,AD=4,抛物线顶点为边AD的中点E,且B,C两点在抛物线上,则从矩形内任取一点落在抛物线与边BC围成的封闭区域(包含边界上的点)内的概率是$\frac{2}{3}$.
如图所示矩形ABCD边长AB=1,AD=4,抛物线顶点为边AD的中点E,且B,C两点在抛物线上,则从矩形内任取一点落在抛物线与边BC围成的封闭区域(包含边界上的点)内的概率是$\frac{2}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com