练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，，P，Q是椭圆上的两点（点Q在第一象限），且直线PM，QM的斜率互为相反数．若，则直线QM的斜率为__________．

    【答案】

    【解析】

    延长，交椭圆于点，由椭圆的对称性和直线PM，QM的斜率互为相反数可知：，设出直线的斜率，写出直线的直线方程，将直线方程与椭圆方程联立，消得到一元二次方程，结合,利用一元二次方程根与系数的关系，求出点坐标，并代入椭圆方程中，求出直线的斜率，也就能求出直线QM的斜率.

    延长，交椭圆于点，由椭圆的对称性和直线PM，QM的斜率互为相反数可知：，如下图所示：

    设直线的斜率为，所以直线的方程为：，与椭圆方程联立得：，消元得，，

    设，根据根与系数关系可得：，

    ，，

    所以，把代入椭圆方程中得，，解得，

    所以直线QM的斜率为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某创业者计划在某旅游景区附近租赁一套农房发展成特色“农家乐”，为了确定未来发展方向此创业者对该景区附近五家“农家乐”跟踪调查了100天，这五家“农家乐的收费标准互不相同得到的统计数据如下表，x为收费标准(单位:元/日)，t为入住天数(单位:天)，以频率作为各自的“入住率”，收费标准x与“入住率”y的散点图如图

    x

    100

    150

    200

    300

    450

    t

    90

    65

    45

    30

    20

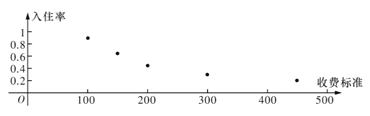
    (1)若从以上五家“农家乐”中随机抽取两家深人调查，记为“入住率超过0.6的农家乐的个数，求的概率分布列

    (2)z＝lnx，由散点图判断与哪个更合适于此模型(给出判断即可不必说明理由)?并根据你的判断结果求回归方程(a，的结果精确到0.1)

    (3)根据第(2)问所求的回归方程，试估计收费标准为多少时，100天销售额L最大?(100天销售额L＝100×入住率×收费标准x)

    参考数据， ，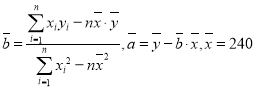

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的某种容器的体积为，它是由圆锥和圆柱两部分连结而成的，圆柱与圆锥的底面圆半径都为.圆锥的高为，母线与底面所成的角为；圆柱的高为.已知圆柱底面造价为元，圆柱侧面造价为元，圆锥侧面造价为元.

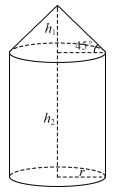
    （1）将圆柱的高表示为底面圆半径的函数，并求出定义域；

    （2）当容器造价最低时，圆柱的底面圆半径为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数.

    （1）讨论函数的单调性；

    （2）当时，方程在区间内有唯一实数解，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直四棱柱中，底面为等腰梯形， ， ， ， ， 、、分别是棱、、的中点.

    （1）证明：直线平面；

    （2）求证：面面.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的标准方程是.

    （1）求它的焦点坐标和准线方程；

    （2）直线过已知抛物线的焦点且倾斜角为45°，且与抛物线的交点为，求的长度.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以下命题中：

    ①若向量、、是空间的一组基底，则向量、、也是空间的一组基底；

    ②已知、、三点不共线，点为平面外任意一点，若点满足，则点平面；

    ③曲线与曲线（且）有相同的焦点.

    ④过定圆上一定点作圆的动弦，为坐标原点，若，则动点的轨迹为椭圆；

    ⑤若过点的直线交椭圆于不同的两点，且是的中点，则直线的方程是.

    其中真命题的序号是______.（写出所有真命题的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解春季昼夜温差大小与某种子发芽数之间的关系，现在从4月份的30天中随机挑选了5天进行研究，且分别记录了明天昼夜温差与每天100颗种子浸泡后的发芽数，得到如下表格：

    日期

    4月1日

    4月7日

    4月15日

    4月21日

    4月30日

    温差x/℃

    10

    11

    13

    12

    8

    发芽数y/颗

    23

    25

    30

    26

    16

    从这5天中任选2天，记发芽的种子数分别为，求事件“君不小于25”的概率；

    （2）从这5天中任选2天，若选取的是4月1日与4月30日的两组数据，请根据这5填中的另三天的数据，求出关于的线性回归方程，.

    （参考公式：，）.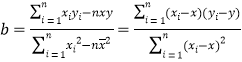

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P-ABCD中，底面ABCD为正方形，平面PAD⊥平面ABCD，点M在线段PPD//平面MAC，PA=PD=，AB=4．

    （I）求证：M为PB的中点；

    （II）求二面角B-PD-A的大小；

    （III）求直线MC与平面BDP所成角的正弦值．

    查看答案和解析>>

    同步练习册答案