
【题目】已知函数f(x)=lnx﹣mx(m∈R).
(1)若曲线y=f(x)过点P(1,﹣1),求曲线y=f(x)在点P处的切线方程;
(2)求函数f(x)在区间[1,e]上的最大值;
(3)若函数f(x)有两个不同的零点x1 , x2 , 求证:x1x2>e2 .
【答案】
(1)解:因为点P(1,﹣1)在曲线y=f(x)上,
所以﹣m=﹣1,解得m=1.
因为f′(x)= ![]() ﹣1=0,
﹣1=0,
所以切线的斜率为0,
所以切线方程为y=﹣1
(2)解:因为f′(x)= ![]() ﹣m=
﹣m= ![]() .
.
①当m≤0时,x∈(1,e),f′(x)>0,
所以函数f (x)在(1,e)上单调递增,
则f (x)max=f (e)=1﹣me.
②当 ![]() ≥e,即0<m≤
≥e,即0<m≤ ![]() 时,x∈(1,e),f′(x)>0,
时,x∈(1,e),f′(x)>0,
所以函数f (x)在(1,e)上单调递增,
则f (x)max=f (e)=1﹣me.
③当1< ![]() <e,即
<e,即 ![]() <m<1时,
<m<1时,
函数f (x)在 (1, ![]() )上单调递增,在(
)上单调递增,在( ![]() ,e)上单调递减,
,e)上单调递减,
则f (x)max=f ( ![]() )=﹣lnm﹣1.
)=﹣lnm﹣1.
④当 ![]() ≤1,即m≥1时,x∈(1,e),f′(x)<0,
≤1,即m≥1时,x∈(1,e),f′(x)<0,
函数f (x)在(1,e)上单调递减,
则f (x)max=f (1)=﹣m.
综上,①当m≤ ![]() 时,f (x)max=1﹣me;
时,f (x)max=1﹣me;
②当 ![]() <m<1时,f (x)max=﹣lnm﹣1;
<m<1时,f (x)max=﹣lnm﹣1;
③当m≥1时,f (x)max=﹣m
(3)解:不妨设x1>x2>0.
因为f (x1)=f (x2)=0,
所以lnx1﹣mx1=0,lnx2﹣mx2=0,
可得lnx1+lnx2=m(x1+x2),lnx1﹣lnx2=m(x1﹣x2).
要证明x1x2>e2,
即证明lnx1+lnx2>2,也就是m(x1+x2)>2.
因为m= ![]() ,
,
所以即证明 ![]() >
> ![]() ,
,
即ln ![]() >
> ![]() .
.
令 ![]() =t,则t>1,于是lnt>
=t,则t>1,于是lnt> ![]() .
.
令(t)=lnt﹣ ![]() (t>1),
(t>1),
则′(t)= ![]() ﹣
﹣ ![]() =
= ![]() >0.
>0.
故函数(t)在(1,+∞)上是增函数,
所以(t)>(1)=0,即lnt> ![]() 成立.
成立.
所以原不等式成立
【解析】(1)中求出斜率,代入切线方程即可;(2)中需要讨论m的范围,m的取值范围不一样,求出的最值不同;(3)中将所证的结论转化为求新函数的单调区间问题得以解决.
【考点精析】掌握利用导数研究函数的单调性和函数的最大(小)值与导数是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且a1=1,an+1=![]() Sn(n=1,2,3,…).
Sn(n=1,2,3,…).
(1)求数列{an}的通项公式;
(2)当bn=![]() (3an+1)时,求证:数列
(3an+1)时,求证:数列![]() 的前n项和Tn=
的前n项和Tn=![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下说法正确的有( )
(1)y=x+ ![]() (x∈R)最小值为2;
(x∈R)最小值为2;
(2)a2+b2≥2ab对a,b∈R恒成立;
(3)a>b>0且c>d>0,则必有ac>bd;
(4)命题“x∈R,使得x2+x+1≥0”的否定是“x∈R,使得x2+x+1≥0”;
(5)实数x>y是 ![]() <
< ![]() 成立的充要条件;
成立的充要条件;
(6)设p,q为简单命题,若“p∨q”为假命题,则“¬p∨¬q”也为假命题.
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)求第3,4,5组的频率;
(2)为了了解最优秀学生的情况,该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试.
查看答案和解析>>
科目:高中数学 来源: 题型:
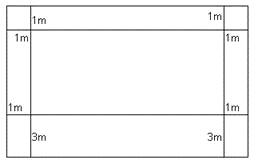
【题目】某村计划建造一个室内面积为800平米的矩形蔬菜温室,在温室内沿左右两侧与后墙内侧各保留1米的通道,沿前侧内墙保留3米宽的空地,当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大的种植面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x),y=g(x)的值域均为R,有以下命题:
①若对于任意x∈R都有f[f(x)]=f(x)成立,则f(x)=x.
②若对于任意x∈R都有f[f(x)]=x成立,则f(x)=x.
③若存在唯一的实数a,使得f[g(a)]=a成立,且对于任意x∈R都有g[f(x)]=x2﹣x+1成立,则存在唯一实数x0 , 使得g(ax0)=1,f(x0)=a.
④若存在实数x0 , y0 , f[g(x0)]=x0 , 且g(x0)=g(y0),则x0=y0 .
其中是真命题的序号是 . (写出所有满足条件的命题序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|x﹣a|的定义域为D,其中a为常数;
(1)若D=R,且f(x)是奇函数,求a的值;
(2)若a≤﹣1,D=[﹣1,0],函数f(x)的最小值是g(a),求g(a)的最大值;
(3)若a>0,在[0,3]上存在n个点xi(i=1,2,…,n,n≥3),满足x1=0,xn=3,x1<x2<…<xn , 使|f(x1)﹣f(x2)|+|f(x2)﹣f(x3)|+…+|f(xn﹣1)﹣f(xn)|= ![]() ,求实数a的取值.
,求实数a的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且a1=a(a∈R),an+1= ![]() ,n∈N*;
,n∈N*;
(1)若0<an≤6,求证:0<an+1≤6;
(2)若a=5,求S2016;
(3)若a= ![]() (m∈N*),求S4m+2的值.
(m∈N*),求S4m+2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,其中a,b,c∈R.
,其中a,b,c∈R.
(1)若a=b=c=1,求f(x)的单调区间;
(2)若b=c=1,且当x≥0时,f(x)≥1恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com