
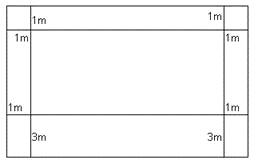
【题目】某村计划建造一个室内面积为800平米的矩形蔬菜温室,在温室内沿左右两侧与后墙内侧各保留1米的通道,沿前侧内墙保留3米宽的空地,当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大的种植面积是多少?
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin(x+ ![]() )图象上各点的横坐标缩短到原来的
)图象上各点的横坐标缩短到原来的 ![]() 倍(纵坐标不变),再把得到的图象向右平移
倍(纵坐标不变),再把得到的图象向右平移 ![]() 个单位,得到的新图象的函数解析式为g(x)= , g(x)的单调递减区间是 .
个单位,得到的新图象的函数解析式为g(x)= , g(x)的单调递减区间是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点F,C上一点
的焦点F,C上一点![]() 到焦点的距离为5.
到焦点的距离为5.
(1)求C的方程;
(2)过F作直线l,交C于A,B两点,若直线AB中点的纵坐标为![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在(﹣4,4)上的奇函数,满足f(2)=1,当﹣4<x≤0时,有f(x)=![]() .
.
(1)求实数a,b的值;
(2)若f(m+1)+![]() >0.求m的取值范围.
>0.求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣mx(m∈R).
(1)若曲线y=f(x)过点P(1,﹣1),求曲线y=f(x)在点P处的切线方程;
(2)求函数f(x)在区间[1,e]上的最大值;
(3)若函数f(x)有两个不同的零点x1 , x2 , 求证:x1x2>e2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为1的半圆O与等边三角形ABC夹在两平行线l1 , l2之间,l∥l1 , l与半圆相交于F,G两点,与三角形ABC两边相交于E,D两点.设弧 ![]() 的长为x(0<x<π),y=EB+BC+CD,若l从l1平行移动到l2 , 则函数y=f(x)的图象大致是( )
的长为x(0<x<π),y=EB+BC+CD,若l从l1平行移动到l2 , 则函数y=f(x)的图象大致是( ) 
A.
B.
C.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足f(x+y)=f(x)·f(y),且f(1)=![]() .
.
(1)当n∈N+,求f(n)的表达式;
(2)设an=nf(n),n∈N+,求证:a1+a2+…+an<2.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)利用f(x+y)=f(x)f(y)(x,y∈R)通过令x=n,y=1,说明{f(n)}是以f(1)=![]() 为首项,公比为
为首项,公比为![]() 的等比数列求出
的等比数列求出![]() ;(2)利用(1)求出an=nf(n)的表达式,利用错位相减法求出数列的前n项和,即可说明不等式成立.
;(2)利用(1)求出an=nf(n)的表达式,利用错位相减法求出数列的前n项和,即可说明不等式成立.
(1)解:f(n)=f[(n-1)+1]
=f(n-1)·f(1)=![]() f(n-1).
f(n-1).
∴当n≥2时,![]() =
=![]() .
.
又f(1)=![]() ,
,
∴数列{f(n)}是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,
∴f(n)=f(1)·(![]() )n-1=(
)n-1=(![]() )n.
)n.
(2)证明:由(1)可知,
an=n·(![]() )n=n·
)n=n·![]() ,
,
设Sn=a1+a2+…+an,
则Sn=![]() +2×
+2×![]() +3×
+3×![]() +…+(n-1)·
+…+(n-1)·![]() +n·
+n·![]() ,①
,①
∴![]() Sn=
Sn=![]() +2×
+2×![]() +…+(n-2)·
+…+(n-2)·![]() +(n-1)·
+(n-1)·![]() +n·
+n·![]() .②
.②
①-②得,
![]() Sn=
Sn=![]() +
+![]() +
+![]() +…+
+…+![]() -n·
-n·![]()
=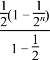 -
-![]() =1-
=1-![]() -
-![]() ,
,
∴Sn=2-![]() -
-![]() <2.
<2.
即a1+a2+…+an<2.
【点睛】
本题考查数列与函数的关系,数列通项公式的求法和的求法,考查不等式的证明,裂项法与错位相减法的应用,数列通项的求法中有常见的已知![]() 和
和![]() 的关系,求
的关系,求![]() 表达式,一般是写出
表达式,一般是写出![]() 做差得通项,但是这种方法需要检验n=1时通项公式是否适用;数列求和常用法有:错位相减,裂项求和,分组求和等.
做差得通项,但是这种方法需要检验n=1时通项公式是否适用;数列求和常用法有:错位相减,裂项求和,分组求和等.
【题型】解答题
【结束】
22
【题目】设数列{an}的前n项和为Sn.已知a1=a (a≠3),an+1=Sn+3n,n∈N+.
(1)设bn=Sn-3n,求数列{bn}的通项公式;
(2)若an+1≥an,n∈N+,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com