
【题目】已知抛物线![]() 的焦点F,C上一点
的焦点F,C上一点![]() 到焦点的距离为5.
到焦点的距离为5.
(1)求C的方程;
(2)过F作直线l,交C于A,B两点,若直线AB中点的纵坐标为![]() ,求直线l的方程.
,求直线l的方程.
【答案】(1)![]() .
.
(2)![]() .
.
【解析】
![]() 法一:利用已知条件列出方程组,求解即可
法一:利用已知条件列出方程组,求解即可
法二:利用抛物线![]() 的准线方程,由抛物线的定义列出方程,求解即可
的准线方程,由抛物线的定义列出方程,求解即可
![]() 法一:由
法一:由![]() 可得抛物线焦点
可得抛物线焦点![]() 的坐标,设出
的坐标,设出![]() 两点的坐标,利用点差法,求出线段
两点的坐标,利用点差法,求出线段![]() 中点的纵坐标为
中点的纵坐标为![]() ,得到直线的斜率,求出直线方程
,得到直线的斜率,求出直线方程
法二:设直线![]() 的方程为
的方程为![]() ,联立直线与抛物线方程,设出
,联立直线与抛物线方程,设出![]() 两点的坐标,通过线段
两点的坐标,通过线段![]() 中点的纵坐标为
中点的纵坐标为![]() ,求出
,求出![]() 即可
即可
法一:抛物线![]() :
: ![]() 的焦点
的焦点![]() 的坐标为
的坐标为![]() ,由已知
,由已知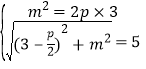
解得![]() 或
或![]() ∵
∵![]() ,
,
∴![]() ∴
∴![]() 的方程为
的方程为![]() .
.
法二:抛物线![]() 的准线方程为
的准线方程为![]() 由抛物线的定义可知
由抛物线的定义可知![]() 解得
解得![]()
∴![]() 的方程为
的方程为![]() .
.
2.法一:由(1)得抛物线C的方程为![]() ,焦点
,焦点![]()
设![]() 两点的坐标分别为
两点的坐标分别为![]() ,则
,则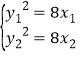
两式相减,整理得![]()
∵线段![]() 中点的纵坐标为
中点的纵坐标为![]()
∴直线![]() 的斜率
的斜率![]()
直线![]() 的方程为
的方程为![]() 即
即![]()
分法二:由(1)得抛物线![]() 的方程为
的方程为![]() ,焦点
,焦点![]()
设直线![]() 的方程为
的方程为![]() 由
由![]()
消去![]() ,得
,得![]() 设
设![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,
∵线段![]() 中点的纵坐标为
中点的纵坐标为![]() ∴
∴![]() 解得
解得![]()
直线![]() 的方程为
的方程为![]() 即
即![]()


科目:高中数学 来源: 题型:
【题目】某网店经营的一种商品进行进价是每件10元,根据一周的销售数据得出周销售量![]() (件)与单价
(件)与单价![]() (元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
(元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.

(1)根据周销售量图写出![]() (件)与单价
(件)与单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)写出利润![]() (元)与单价
(元)与单价![]() (元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,且tanC= ![]() ,c=﹣3bcosA.
,c=﹣3bcosA.
(1)求tanB的值;
(2)若c=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面几何里,有“若△ABC的三边长分别为a,b,c,内切圆半径为r,则三角形面积为S△ABC=![]() (a+b+c)r”,拓展到空间,类比上述结论,“若四面体ABCD的四个面的面积分别为S1,S2,S3,S4,内切球的半径为r,则四面体的体积为________”.
(a+b+c)r”,拓展到空间,类比上述结论,“若四面体ABCD的四个面的面积分别为S1,S2,S3,S4,内切球的半径为r,则四面体的体积为________”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB= ![]() ,BC=1,P为△ABC内一点,∠BPC=90°
,BC=1,P为△ABC内一点,∠BPC=90° 
(1)若PB= ![]() ,求PA;
,求PA;
(2)若∠APB=150°,求tan∠PBA.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下说法正确的有( )
(1)y=x+ ![]() (x∈R)最小值为2;
(x∈R)最小值为2;
(2)a2+b2≥2ab对a,b∈R恒成立;
(3)a>b>0且c>d>0,则必有ac>bd;
(4)命题“x∈R,使得x2+x+1≥0”的否定是“x∈R,使得x2+x+1≥0”;
(5)实数x>y是 ![]() <
< ![]() 成立的充要条件;
成立的充要条件;
(6)设p,q为简单命题,若“p∨q”为假命题,则“¬p∨¬q”也为假命题.
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校高三数学备课组为了更好地制定复习计划,开展了试卷讲评后效果的调研,从上学期期末数学试题中选出一些学生易错题,重新进行测试,并认为做这些题不出任何错误的同学为“过关”,出了错误的同学为“不过关”,现随机抽查了年级50人,他们的测试成绩的频数分布如下表:
期末分数段 |
|
|
|
|
|
|
人数 | 5 | 10 | 15 | 10 | 5 | 5 |
“过关”人数 | 1 | 2 | 9 | 7 | 3 | 4 |
(1)由以上统计数据完成如下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为期末数学成绩不低于90分与测试“过关”有关?说明你的理由:
的把握认为期末数学成绩不低于90分与测试“过关”有关?说明你的理由:
分数低于90分人数 | 分数不低于90分人数 | 合计 | |
“过关”人数 | |||
“不过关”人数 | |||
合计 |
(2)在期末分数段![]() 的5人中,从中随机选3人,记抽取到过关测试“过关”的人数为
的5人中,从中随机选3人,记抽取到过关测试“过关”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |

查看答案和解析>>
科目:高中数学 来源: 题型:
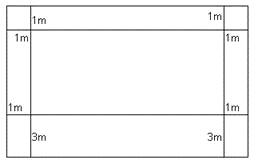
【题目】某村计划建造一个室内面积为800平米的矩形蔬菜温室,在温室内沿左右两侧与后墙内侧各保留1米的通道,沿前侧内墙保留3米宽的空地,当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大的种植面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是函数
是函数![]() 的反函数,函数
的反函数,函数![]() 的图像关于直线
的图像关于直线![]() 对称,记
对称,记![]() .
.
(1)求函数![]() 的解析式和定义域﹔
的解析式和定义域﹔
(2)在![]() 的图像上是否存在这样两个不同点A,B,使直线AB恰好与y轴垂直?若存在,求A,B的坐标;若不存在,说明理由.
的图像上是否存在这样两个不同点A,B,使直线AB恰好与y轴垂直?若存在,求A,B的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com