
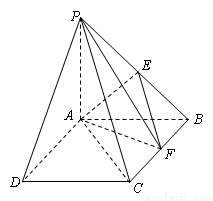
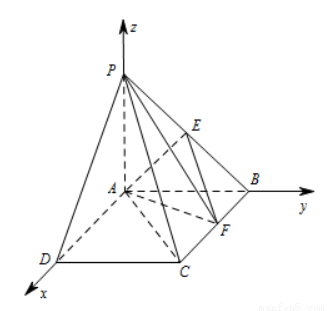
(本小题满分14分)如图,在四棱锥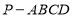 中,底面
中,底面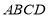 是正方形,侧面
是正方形,侧面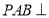 底面
底面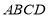 ,
, 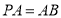 ,点
,点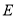 是
是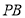 的中点,点
的中点,点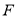 在边
在边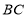 上移动.
上移动.
(Ⅰ)若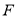 为
为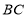 中点,求证:
中点,求证: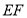 //平面
//平面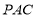 ;
;
(Ⅱ)求证: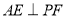 ;
;
(Ⅲ)若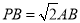 ,二面角
,二面角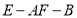 的余弦值等于
的余弦值等于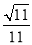 ,试判断点
,试判断点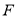 在边
在边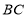 上的位置,并说明理由.
上的位置,并说明理由.
(1)证明详见解析;(2)证明详见解析;(3)点F为边BC上靠近B点的三等分点.
【解析】
试题分析:本题主要考查线线平行、线面平行、线线垂直、线面垂直、二面角、向量法等基础知识,考查学生的分析问题解决问题的能力、空间想象能力、逻辑推理能力.第一问,在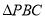 中,E、F分别是BP、BC中点,利用中位线的性质得
中,E、F分别是BP、BC中点,利用中位线的性质得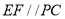 ,再根据线面平行的判定得出结论;第二问,由正方形ABCD得出
,再根据线面平行的判定得出结论;第二问,由正方形ABCD得出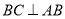 ,利用面面垂直的性质,得
,利用面面垂直的性质,得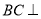 平面PAB,利用线面垂直的性质,得
平面PAB,利用线面垂直的性质,得 ,再从
,再从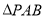 中证出
中证出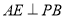 ,利用线面垂直的判定得
,利用线面垂直的判定得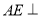 平面PBC,所以AE垂直面PBC内的线PF;第三问,利用已知的这些条件整理出AD、AB、AP两两垂直,建立空间直角坐标系,写出相关点的坐标,得出向量坐标,分别求出平面AEF和平面ABF的法向量,利用夹角公式列出表达式,求出m,即得到BF的长,从而得到点F的位置.
平面PBC,所以AE垂直面PBC内的线PF;第三问,利用已知的这些条件整理出AD、AB、AP两两垂直,建立空间直角坐标系,写出相关点的坐标,得出向量坐标,分别求出平面AEF和平面ABF的法向量,利用夹角公式列出表达式,求出m,即得到BF的长,从而得到点F的位置.
试题解析:(1)在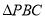 中,∵点E是PB中点,点F是BC中点,
中,∵点E是PB中点,点F是BC中点,
∴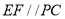 ,
,
又∵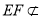 平面PAC,
平面PAC,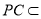 平面PAC,
平面PAC,
∴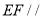 平面PAC.
平面PAC.
(2)∵底面ABCD是正方形,∴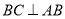 .
.
又∵侧面PAB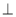 底面ABCD,平面PAB
底面ABCD,平面PAB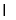 平面ABCD=AB,且
平面ABCD=AB,且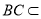 平面ABCD,
平面ABCD,
∴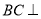 平面PAB.
平面PAB.
∵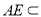 平面PAB,
平面PAB,
∴ ,
,
由已知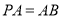 ,点E是PB的中点,
,点E是PB的中点,
∴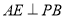 ,
,
又∵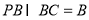 ,
,
∴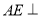 平面PBC.
平面PBC.
∵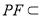 平面PBC,
平面PBC,
∴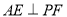 .
.
(3)点F为边BC上靠近B点的三等分点.
∵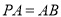 ,
,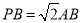 ,
,
∴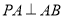 ,
,
由(2)可知,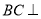 平面PAB.
平面PAB.
又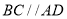 ,
,
∴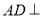 平面PAB,即
平面PAB,即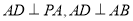 ,
,
∴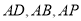 两两垂直.
两两垂直.
分别以AD,AB,AP为x轴,y轴,z轴,建立空间直角坐标系(如图).
不妨设 ,则
,则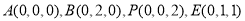 ,
, .
.
∴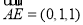 ,
,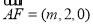 .
.
设平面AEF的一个法向量为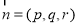 ,
,
∵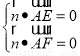 ,得
,得 ,取
,取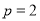 ,则
,则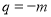 ,
,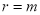 ,得
,得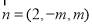 .
.
∵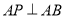 ,
,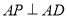 ,
,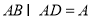 ,
,
∴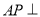 平面ABCD.
平面ABCD.
即平面ABF的一个法向量为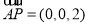 .
.
∴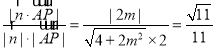 ,解得
,解得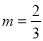 .
.
∵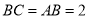 ,
,
∴ ,即点F为边BC上靠近B点的三等分点.
,即点F为边BC上靠近B点的三等分点.
考点:线线平行、线面平行、线线垂直、线面垂直、二面角、向量法.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源:2014-2015学年北京市大兴区高三上学期期末考试理科数学试卷(解析版) 题型:选择题
已知集合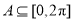 ,集合
,集合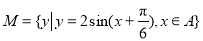 ,若
,若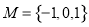 ,则不同集合A的个数是
,则不同集合A的个数是
(A)12 (B)27
(C)42 (D)63
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市朝阳区高三上学期期末考试理科数学试卷(解析版) 题型:填空题
设不等式组 表示平面区域为
表示平面区域为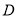 ,在区域
,在区域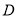 内随机取一点
内随机取一点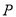 ,则点
,则点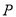 落在圆
落在圆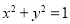 内的概率为 .
内的概率为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市朝阳区高三上学期期末考试理科数学试卷(解析版) 题型:选择题
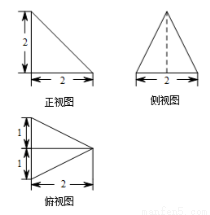
某三棱锥的三视图如图所示,则该三棱锥的全面积是( )
A.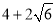 B.
B.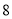 C.
C.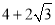 D.
D.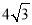
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山西省高二上学期期末理科数学试卷(解析版) 题型:选择题
如图1,正方体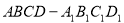 中,PQ是异面直线
中,PQ是异面直线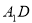 与AC的公垂线,则直线PQ与
与AC的公垂线,则直线PQ与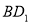 的位置关系为( )
的位置关系为( )
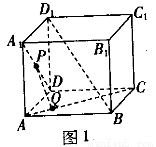
A.平行 B.异面 C.相交 D.无法判断
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com