
已知数列 前n项和
前n项和 =
= (
(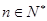 ), 数列
), 数列 为等比数列,首项
为等比数列,首项 =2,公比为q(q>0)且满足
=2,公比为q(q>0)且满足 ,
, ,
, 为等比数列.
为等比数列.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)设 ,记数列
,记数列 的前n项和为Tn,,求Tn。
的前n项和为Tn,,求Tn。
(1)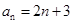 ,
, ;(2)
;(2)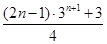
解析试题分析:(1)因为数列 前n项和
前n项和 =
= (
(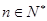 ),这类型一般都是通过向前递推一个等式,然后根据
),这类型一般都是通过向前递推一个等式,然后根据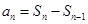 .即可转化为关于通项的等式.但是要检验第一项是否成立.数列
.即可转化为关于通项的等式.但是要检验第一项是否成立.数列 为等比数列以及题所给的其他条件,即可求出通项公式.
为等比数列以及题所给的其他条件,即可求出通项公式.
(2)因为 ,又因为由(1)可得
,又因为由(1)可得 ,
, 的通项公式,即可求得数列
的通项公式,即可求得数列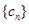 的通项公式.再通过错位相减法求得前n项的和.
的通项公式.再通过错位相减法求得前n项的和.
试题解析:(1)当n=1时, .
.
当n≥2时,
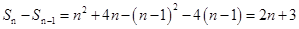 ,
,
验证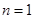 时也成立.∴数列
时也成立.∴数列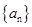 的通项公式为:
的通项公式为: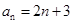 ,
,
∵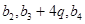 成等差数列,
成等差数列,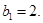 所以
所以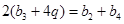 ,即
,即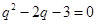 ,
,
因为 ∴
∴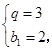 ∴数列
∴数列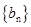 的通项公式为:
的通项公式为: 6分
6分
(2)∵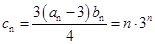
∴ 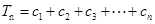
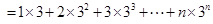 ①
① ②
②
由①-②得: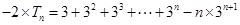
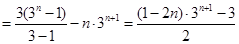
∴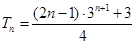 12分
12分
考点:1.数列的通项与前n项和的关系式.2.等比数列.3.错位相减法.4.递推的数学思想.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
已知数列{an}满足a1=3,an+1=an+p·3n(n∈N*,p为常数),a1,a2+6,a3成等差数列.
(1)求p的值及数列{an}的通项公式;
(2)设数列{bn}满足bn=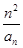 ,证明:bn≤
,证明:bn≤ .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
观察下列三角形数表,假设第n行的第二个数为an(n≥2,n∈N*).
(1)依次写出第六行的所有6个数;
(2)归纳出an+1与an的关系式并求出{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于任意的 (
( 不超过数列的项数),若数列的前
不超过数列的项数),若数列的前 项和等于该数列的前
项和等于该数列的前 项之积,则称该数列为
项之积,则称该数列为 型数列。
型数列。
(1)若数列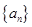 是首项
是首项 的
的 型数列,求
型数列,求 的值;
的值;
(2)证明:任何项数不小于3的递增的正整数列都不是 型数列;
型数列;
(3)若数列 是
是 型数列,且
型数列,且 试求
试求 与
与 的递推关系,并证明
的递推关系,并证明 对
对 恒成立。
恒成立。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com