
【题目】已知![]() .
.
(1)当![]() 时,若
时,若![]() 恰有一个零点,求实数
恰有一个零点,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由解析式确定定义域,当![]() 时,表示此时的
时,表示此时的![]() 表达式并求导,利用分类讨论参数a,进而分析零点情况;当
表达式并求导,利用分类讨论参数a,进而分析零点情况;当![]() 时,显然无零点,不符合题意;当
时,显然无零点,不符合题意;当![]() 时,由零点的存在性定理可证得只有一个零点,符合题意;当
时,由零点的存在性定理可证得只有一个零点,符合题意;当![]() 时,
时,![]() 在
在![]() 单减,在
单减,在![]() 单增,进而只有一个零点即
单增,进而只有一个零点即![]() ,解得
,解得![]() ,综上可得答案;
,综上可得答案;
(2)令![]() ,
,![]() 恒成立等价于
恒成立等价于![]() 恒成立,进而利用分类讨论思想借助导数表示
恒成立,进而利用分类讨论思想借助导数表示![]() ,求得答案.
,求得答案.
定义域:![]() .
.
(1)当![]() 时,
时,![]() ,
, .
.
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 单增,
单增,![]() ,∴
,∴![]() 在
在![]() 无零点;
无零点;
②当![]() 时,
时,![]() ,
,![]() 在
在![]() 单增,又
单增,又![]() ,由
,由![]() ,
,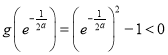 ,
,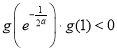 ,∴
,∴![]() 在
在![]() 恰有一个零点;
恰有一个零点;
③当![]() 时,
时,![]() ,
,![]() 在
在![]() 单减,在
单减,在![]() 单增,
单增,
要使![]() 在
在![]() 恰有一个零点,则
恰有一个零点,则![]() ,解得
,解得![]()
综上所述,若![]() 恰有一个零点,则
恰有一个零点,则![]() 或
或![]() ,即实数
,即实数![]() 的范围是
的范围是![]() .
.
(2)令![]() ,
,
![]() ,又
,又![]() ,要使
,要使![]() 在
在![]() 恒成立.
恒成立.
①当![]() 时,
时,![]() 在
在![]() 单减,在
单减,在![]() 单增,虽然
单增,虽然![]() ,
,
但当![]() 时
时![]() ,所以
,所以![]() 在
在![]() 恒成立不成立,
恒成立不成立,![]() 不合题意.
不合题意.
②当![]() 时,
时,![]() 在
在![]() 恒成立,
恒成立,![]() 在
在![]() 单增,虽然
单增,虽然![]() ,
,
但当![]() 时
时![]() ,所以
,所以![]() 在
在![]() 恒成立不成立,
恒成立不成立,![]() 不合题意.
不合题意.
③当![]() 时,
时,![]() 在
在![]() 恒成立,
恒成立,![]() 在
在![]() 单减,所以要使
单减,所以要使![]() 在
在![]() 恒成立的充要条件是
恒成立的充要条件是![]() ,即
,即![]() ,解得
,解得![]() ,故
,故![]() .
.
综上所述,实数![]() 的范围是
的范围是![]() ,即实数
,即实数![]() 的范围
的范围![]() .
.


科目:高中数学 来源: 题型:
【题目】某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段![]() 进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如下):
进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如下):

(Ⅰ)体育成绩大于或等于70分的学生常被称为“体育良好”.已知该校高一年级有1000名学生,试估计高一全年级中“体育良好”的学生人数;
(Ⅱ)为分析学生平时的体育活动情况,现从体育成绩在![]() 和
和![]() 的样本学生中随机抽取2人,求在抽取的2名学生中,至少有1人体育成绩在
的样本学生中随机抽取2人,求在抽取的2名学生中,至少有1人体育成绩在![]() 的概率;
的概率;
(Ⅲ)假设甲、乙、丙三人的体育成绩分别为![]() 且分别在
且分别在![]() 三组中,其中
三组中,其中![]() 当数据
当数据![]() 的方差
的方差![]() 最小时,写出
最小时,写出![]() 的值.(结论不要求证明)
的值.(结论不要求证明)
(注: ![]() ,其中
,其中![]() 为数据
为数据![]() 的平均数)
的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,底面
,底面![]() 为梯形,
为梯形,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
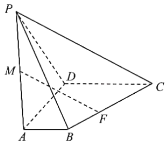
(I)求证:![]() ;
;
(II)求二面角_____的余弦值;
从①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在上面问题中并作答.注:如果选择多个条件分别解答,按第一个解答计分.
这三个条件中任选一个,补充在上面问题中并作答.注:如果选择多个条件分别解答,按第一个解答计分.
(III)若![]() 是棱
是棱![]() 的中点,求证:对于棱
的中点,求证:对于棱![]() 上任意一点
上任意一点![]() ,
,![]() 与
与![]() 都不平行.
都不平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】赵爽是我国古代数学家、天文学家,大约公元222年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,又称“赵爽弦图”(以弦为边长得到的正方形是由![]() 个全等的直角三角形再加上中间的一个小正方形组成的,如图(1)),类比“赵爽弦图”,可类似地构造如图(2)所示的图形,它是由
个全等的直角三角形再加上中间的一个小正方形组成的,如图(1)),类比“赵爽弦图”,可类似地构造如图(2)所示的图形,它是由![]() 个全等的三角形与中间的一个小正六边形组成的一个大正六边形,设
个全等的三角形与中间的一个小正六边形组成的一个大正六边形,设![]() ,若在大正六边形中随机取一点,则此点取自小正六边形的概率为( )
,若在大正六边形中随机取一点,则此点取自小正六边形的概率为( )
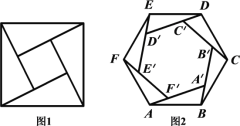
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全面抗击新冠肺炎疫情这一特殊时期,我市教育局提出“停课不停学”的口号,鼓励学生线上学习.某校数学教师为了调查高三学生数学成绩与线上学习时间之间的相关关系,对高三年级随机选取45名学生进行跟踪问卷,其中每周线上学习数学时间不少于5小时的有19人,余下的人中,在检测考试中数学平均成绩不足120分的占![]() ,统计成绩后得到如下
,统计成绩后得到如下![]() 列联表:
列联表:
分数不少于120分 | 分数不足120分 | 合计 | |
线上学习时间不少于5小时 | 4 | 19 | |
线上学习时间不足5小时 | |||
合计 | 45 |
(1)请完成上面![]() 列联表;并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
列联表;并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
(2)①按照分层抽样的方法,在上述样本中从分数不少于120分和分数不足120分的两组学生中抽取9名学生,设抽到不足120分且每周线上学习时间不足5小时的人数是![]() ,求
,求![]() 的分布列(概率用组合数算式表示);
的分布列(概率用组合数算式表示);
②若将频率视为概率,从全校高三该次检测数学成绩不少于120分的学生中随机抽取20人,求这些人中每周线上学习时间不少于5小时的人数的期望和方差.
(下面的临界值表供参考)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式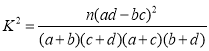 其中
其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的生态文明发展理念已经深入人心,这将推动新能源汽车产业的迅速发展.下表是近几年我国某地区新能源乘用车的年销售量与年份的统计表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
销量(万台) | 8 | 10 | 13 | 25 | 24 |
某机构调查了该地区30位购车车主的性别与购车种类情况,得到的部分数据如下表所示:
购置传统燃油车 | 购置新能源车 | 总计 | |
男性车主 | 6 | 24 | |
女性车主 | 2 | ||
总计 | 30 |
(1)求新能源乘用车的销量![]() 关于年份
关于年份![]() 的线性相关系数
的线性相关系数![]() ,并判断
,并判断![]() 与
与![]() 是否线性相关;
是否线性相关;
(2)请将上述![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为购车车主是否购置新能源乘用车与性别有关;
的把握认为购车车主是否购置新能源乘用车与性别有关;
(3)若以这30名购车车主中购置新能源乘用车的车主性别比例作为该地区购置新能源乘用车的车主性别比例,从该地区购置新能源乘用车的车主中随机选取50人,记选到女性车主的人数为X,求X的数学期望与方差.
参考公式: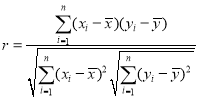 ,
,![]() ,其中
,其中![]() .
.![]() ,若
,若![]() ,则可判断
,则可判断![]() 与
与![]() 线性相关.
线性相关.
附表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
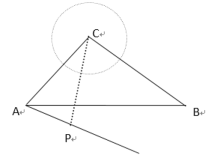
【题目】某工厂C发生爆炸出现毒气泄漏,已知毒气以圆形向外扩散,且半径以每分钟![]() 的速度增大. 一所学校A,位于工厂C南偏西
的速度增大. 一所学校A,位于工厂C南偏西![]() ,且与工厂相距
,且与工厂相距![]() .消防站B位于学校A的正东方向,且位于工厂C南偏东
.消防站B位于学校A的正东方向,且位于工厂C南偏东![]() ,立即以每分钟
,立即以每分钟![]() 的速度沿直线
的速度沿直线![]() 赶往工厂C救援,同时学校组织学生P从A处沿着南偏东
赶往工厂C救援,同时学校组织学生P从A处沿着南偏东![]() 的道路,以每分钟
的道路,以每分钟![]() 的速度进行安全疏散(与爆炸的时间差忽略不计).要想在消防员赶往工厂的时间内(包括消防员到达工厂的时刻),保证学生的安全,学生撤离的速度应满足什么要求?
的速度进行安全疏散(与爆炸的时间差忽略不计).要想在消防员赶往工厂的时间内(包括消防员到达工厂的时刻),保证学生的安全,学生撤离的速度应满足什么要求?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com