
分析 (1)由导数与极值的关系知可转化为方程f′(x)=lnx-ax=0在(0,+∞)有两个不同根;再转化为函数y=lnx与函数y=ax的图象在(0,+∞)上有两个不同交点;
(2)原式等价于 $\frac{ln\frac{{x}_{1}}{{x}_{2}}}{{{x}_{1}-x}_{2}}$>$\frac{1+λ}{{x}_{1}+{λx}_{2}}$,令t=$\frac{{x}_{1}}{{x}_{2}}$,t∈(0,1),则不等式lnt<$\frac{(1+λ)(t-1)}{t+λ}$在t∈(0,1)上恒成立.令h(t)=lnt-$\frac{(1+λ)(t-1)}{t+λ}$,t∈(0,1),
根据函数的单调性求出即可.
解答 解:(1)由题意知,函数f(x)的定义域为(0,+∞),
方程f′(x)=0在(0,+∞)有两个不同根,即方程lnx-ax=0在(0,+∞)有两个不同根;
转化为函数y=lnx与函数y=ax的图象在(0,+∞)上有两个不同交点,
如图示: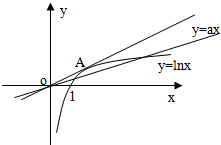 ,
,
可见,若令过原点且切于函数y=lnx图象的直线斜率为k,只须0<a<k.
令切点A(x0,lnx0),
故k=y′|x=x0=$\frac{1}{{x}_{0}}$,又k=$\frac{l{nx}_{0}}{{x}_{0}}$,
故 $\frac{1}{{x}_{0}}$=$\frac{l{nx}_{0}}{{x}_{0}}$,解得,x0=e,
故k=$\frac{1}{e}$,故0<a<$\frac{1}{e}$;
(2)因为e1+λ<x1•x2λ等价于1+λ<lnx1+λlnx2.
由(1)可知x1,x2分别是方程lnx-ax=0的两个根,
即lnx1=ax1,lnx2=ax2
所以原式等价于1+λ<ax1+λax2=a(x1+λx2),因为λ>0,0<x1<x2,
所以原式等价于a>$\frac{1+λ}{{x}_{1}+{λx}_{2}}$,
又由lnx1=ax1,lnx2=ax2作差得,ln $\frac{{x}_{1}}{{x}_{2}}$=a(x1-x2),
所以原式等价于 $\frac{ln\frac{{x}_{1}}{{x}_{2}}}{{{x}_{1}-x}_{2}}$>$\frac{1+λ}{{x}_{1}+{λx}_{2}}$,
因为0<x1<x2,原式恒成立,即ln$\frac{{x}_{1}}{{x}_{2}}$<$\frac{(1+λ){(x}_{1}{-x}_{2})}{{x}_{1}+{λx}_{2}}$恒成立.
令t=$\frac{{x}_{1}}{{x}_{2}}$,t∈(0,1),
则不等式lnt<$\frac{(1+λ)(t-1)}{t+λ}$在t∈(0,1)上恒成立.
令h(t)=lnt-$\frac{(1+λ)(t-1)}{t+λ}$,t∈(0,1),
又h′(t)=$\frac{(t-1)(t{-λ}^{2})}{{t(t+λ)}^{2}}$,
当λ2≥1时,可见t∈(0,1)时,h′(t)>0,
所以h(t)在t∈(0,1)上单调增,又h(1)=0,h(t)<0在t∈(0,1)恒成立,符合题意.
当λ2<1时,可见t∈(0,λ2)时,h′(t)>0,t∈(λ2,1)时h′(t)<0,
所以h(t)在t∈(0,λ2)时单调增,在t∈(λ2,1)时单调减,又h(1)=0,
所以h(t)在t∈(0,1)上不能恒小于0,不符合题意,舍去.
综上所述,若不等式e1+λ<x1•x2λ恒成立,只须λ2≥1,又λ>0,所以λ≥1.
点评 本题考查了导数的综合应用及分类讨论,转化思想,数形结合的思想方法的应用,是一道综合题.


科目:高中数学 来源: 题型:填空题
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
| 韭菜 | 5吨 | 0.9万元 | 0.3万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x3 | B. | y=$\frac{1}{x-1}$ | C. | y=log2$\frac{1}{x}$ | D. | y=-tanx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{10}$ | B. | $\frac{19}{21}$ | C. | $\frac{10}{11}$ | D. | $\frac{11}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向右平移$\frac{π}{8}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向左平移$\frac{π}{8}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
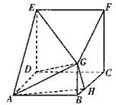 在多面体ABCDEFG中,四边形ABCD与CDEF均为边长为4的正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH.
在多面体ABCDEFG中,四边形ABCD与CDEF均为边长为4的正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
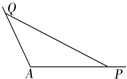 如图,角A为钝角,且sinA=$\frac{3}{5}$,点P、Q分别是在角A的两边上不同于点A的动点.
如图,角A为钝角,且sinA=$\frac{3}{5}$,点P、Q分别是在角A的两边上不同于点A的动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com