
| A. | $\overrightarrow{a}$?$\overrightarrow{b}$=$\overrightarrow{b}$?$\overrightarrow{a}$ | |
| B. | 若$\overrightarrow{a}$?$\overrightarrow{b}$=0,则$\overrightarrow{a}$$∥\overrightarrow{b}$ | |
| C. | ($\overrightarrow{a}$+$\overrightarrow{b}$)?$\overrightarrow{c}$=$\overrightarrow{a}$?$\overrightarrow{c}$+$\overrightarrow{b}$?$\overrightarrow{c}$ | |
| D. | 若$\overrightarrow{a}$=(x1,y1),$\overrightarrow{b}$=(x2,y2),则$\overrightarrow{a}$?$\overrightarrow{b}$=|x1y2-x2y1| |
分析 对于选项A,根据$\overrightarrow{a}$?$\overrightarrow{b}$运算的定义容易判断出选项A恒成立;
对于选项B,讨论$\overrightarrow{a},\overrightarrow{b}$是否为$\overrightarrow{0}$:$\overrightarrow{a},\overrightarrow{b}$都不为$\overrightarrow{0}$时,便可得出sinθ=0,从而得到θ=0,或π,从而得出$\overrightarrow{a}∥\overrightarrow{b}$,而$\overrightarrow{a},\overrightarrow{b}$中有一个为$\overrightarrow{0}$时,显然$\overrightarrow{a}∥\overrightarrow{b}$成立,从而判断出B恒成立;
对于选项C,可设$\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{0}$,而$\overrightarrow{c}$与$\overrightarrow{a},\overrightarrow{b}$不共线,这样即可说明该选项不恒成立;
对于选项D,根据$\overrightarrow{a}?\overrightarrow{b}$运算的定义即可得到$\overrightarrow{a}$?$\overrightarrow{b}$=$|\overrightarrow{a}||\overrightarrow{b}|\sqrt{1-co{s}^{2}θ}$,而$cosθ=\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$,带入化简,并带入$|\overrightarrow{a}|=\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}},|\overrightarrow{b}|=\sqrt{{{x}_{2}}^{2}+{{y}_{2}}^{2}}$便可以说明该选项恒成立,这样即可得出正确选项.
解答 解:A.∵$\overrightarrow{a}$?$\overrightarrow{b}$=$|\overrightarrow{a}|•|\overrightarrow{b}|sinθ$,θ表示向量$\overrightarrow{a},\overrightarrow{b}$的夹角;
$\overrightarrow{a}?\overrightarrow{b}=|\overrightarrow{a}|•|\overrightarrow{b}|sinθ=|\overrightarrow{b}|•|\overrightarrow{a}|sinθ=\overrightarrow{b}?\overrightarrow{a}$,∴该选项恒成立;
B.①当$\overrightarrow{a},\overrightarrow{b}≠\overrightarrow{0}$时,$\overrightarrow{a}$?$\overrightarrow{b}$=$|\overrightarrow{a}|•|\overrightarrow{b}|sinθ=0$时,sinθ=0;
∴θ=0,或π;
∴$\overrightarrow{a}$∥$\overrightarrow{b}$;
②当$\overrightarrow{a}=\overrightarrow{0}$,或$\overrightarrow{b}=\overrightarrow{0}$时,$\overrightarrow{a}∥\overrightarrow{b}$恒成立;
∴该选项恒成立;
C.当$|\overrightarrow{a}|=|\overrightarrow{b}|=|\overrightarrow{c}|=1$,$\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{0}$,$\overrightarrow{c}⊥\overrightarrow{a},\overrightarrow{c}⊥\overrightarrow{b}$时,$(\overrightarrow{a}+\overrightarrow{b})$?$\overrightarrow{c}=0$,$\overrightarrow{a}?\overrightarrow{c}+\overrightarrow{b}?\overrightarrow{c}=2$;
∴该选项不恒成立;
D.$\overrightarrow{a}$?$\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|sinθ=|\overrightarrow{a}||\overrightarrow{b}|\sqrt{1-co{s}^{2}θ}$=$|\overrightarrow{a}||\overrightarrow{b}|\sqrt{1-(\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|})^{2}}$=$\sqrt{|\overrightarrow{a}{|}^{2}|\overrightarrow{b}{|}^{2}-(\overrightarrow{a}•\overrightarrow{b})^{2}}$
=$\sqrt{({{x}_{1}}^{2}+{{y}_{1}}^{2})({{x}_{2}}^{2}+{{y}_{2}}^{2})-({x}_{1}{x}_{2}+{y}_{1}{y}_{2})^{2}}$=$\sqrt{({x}_{1}{y}_{2}-{x}_{2}{y}_{1})^{2}}=|{x}_{1}{y}_{2}-{x}_{2}{y}_{1}|$,∴该选项恒成立.
故选:C.
点评 考查对新运算$\overrightarrow{a}?\overrightarrow{b}$的理解和运用,向量夹角的概念,向量平行的概念,举反例的方法说明结论不恒成立,以及向量夹角的余弦公式,根据向量坐标求向量长度,完全平方公式的运用.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | k | C. | $\frac{k+1+|k-1|}{2}$ | D. | $\frac{k+1-|k-1|}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p是假命题 | B. | q是真命题 | C. | “p∧q”是假命题 | D. | “p∨q”是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
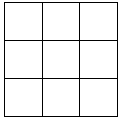 将4个红球与2个蓝球(这些球只有颜色不同,其他完全相同)放入一个3×3的格子状木柜里(如图所示),每个格至多放一个球,则“所有红球均不位于相邻格子”的放法共有( )种.
将4个红球与2个蓝球(这些球只有颜色不同,其他完全相同)放入一个3×3的格子状木柜里(如图所示),每个格至多放一个球,则“所有红球均不位于相邻格子”的放法共有( )种.| A. | 30 | B. | 36 | C. | 60 | D. | 72 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com