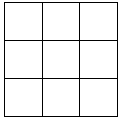
将4个红球与2个蓝球(这些球只有颜色不同.其他完全相同)放入一个3×3的格子状木柜里.每个格至多放一个球.则“所有红球均不位于相邻格子的放法共有( )种．A．30B．36C．60D．72 题目和参考答案——青夏教育精英家教网—

12．

将4个红球与2个蓝球（这些球只有颜色不同，其他完全相同）放入一个3×3的格子状木柜里（如图所示），每个格至多放一个球，则“所有红球均不位于相邻格子”的放法共有（　　）种．

A．

B．

C．

D．

分析对红球的位置分类讨论：第一类，当4个红球在4个顶角的位置时，蓝球放在剩下5个格种任选两个；第二类，当有一个红球再最中间时，其它三个红球只能放在顶角位置，蓝球放在剩下5个格种任选两个；第三类，当4个红球放在每外围三个格的中间时，蓝球放在剩下5个格种任选两个，即可得出．

解答解：第一类，当4个红球在4个顶角的位置时，蓝球放在剩下5个格种任选两个，故有C₅²=10种，如图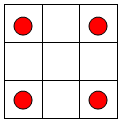

第二类，当有一个红球再最中间时，其它三个红球只能放在顶角位置，有出C₄³=4种，蓝球放在剩下5个格种任选两个，C₄³C₅²=40种，如图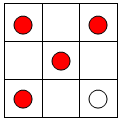

第三类，当4个红球放在每外围三个格的中间时，蓝球在剩下5个格种任选两个有C₅²=10种，如图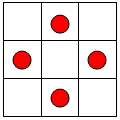

根据分类计数原理，故有10+40+10=60．
故选：C．

点评本题主要考查了分类计数原理，关键是如何分类，属于中档题．

练习册系列答案

高中同步检测优化卷38分钟高效作业本系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

2．对于两个平面向量$\overrightarrow{a}$，$\overrightarrow{b}$，定义它们的一种运算：$\overrightarrow{a}$?$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|sinθ（其中θ为向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角），则关于这种运算的以下结论中，不恒成立的是（　　）

	A．	$\overrightarrow{a}$?$\overrightarrow{b}$=$\overrightarrow{b}$?$\overrightarrow{a}$
	B．	若$\overrightarrow{a}$?$\overrightarrow{b}$=0，则$\overrightarrow{a}$$∥\overrightarrow{b}$
	C．	（$\overrightarrow{a}$+$\overrightarrow{b}$）?$\overrightarrow{c}$=$\overrightarrow{a}$?$\overrightarrow{c}$+$\overrightarrow{b}$?$\overrightarrow{c}$
	D．	若$\overrightarrow{a}$=（x₁，y₁），$\overrightarrow{b}$=（x₂，y₂），则$\overrightarrow{a}$?$\overrightarrow{b}$=\|x₁y₂-x₂y₁\|

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

3．已知函数f（x）=asinx+bcosx，其中a，b为非零实常数．
（1）f（$\frac{π}{4}$）=$\sqrt{2}$，f（x）的最大值为$\sqrt{10}$，求a，b的值；‘
（2）若a=1，x=$\frac{π}{6}$是f（x）的图象的一条对称轴，求x₀的值，使其满足f（x₀）=$\sqrt{3}$，且x₀∈[0，2π]．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题