
分析 直接利用三角函数的定义求解即可.
解答 解:角α的终边上有一点P(-4b,3b)(b≠0),
当b>0时
则sinα=$\frac{3b}{\sqrt{(-4b)^{2}+(3b)^{2}}}$=$\frac{3}{5}$,
cosα=-$\frac{4}{5}$,
则sinα+cosα=-$\frac{1}{5}$.
当b<0时
则sinα=$\frac{3b}{\sqrt{(-4b)^{2}+(3b)^{2}}}$=-$\frac{3}{5}$,
cosα=$\frac{4}{5}$,
则sinα+cosα=$\frac{1}{5}$.
故答案为:$±\frac{1}{5}$.
点评 本题考查任意角的三角函数的定义,考查计算能力.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:选择题
| A. | p是假命题 | B. | q是真命题 | C. | “p∧q”是假命题 | D. | “p∨q”是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
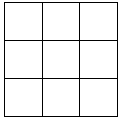 将4个红球与2个蓝球(这些球只有颜色不同,其他完全相同)放入一个3×3的格子状木柜里(如图所示),每个格至多放一个球,则“所有红球均不位于相邻格子”的放法共有( )种.
将4个红球与2个蓝球(这些球只有颜色不同,其他完全相同)放入一个3×3的格子状木柜里(如图所示),每个格至多放一个球,则“所有红球均不位于相邻格子”的放法共有( )种.| A. | 30 | B. | 36 | C. | 60 | D. | 72 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com