
| A. | p是假命题 | B. | q是真命题 | C. | “p∧q”是假命题 | D. | “p∨q”是假命题 |
分析 分别判断出p,q的真假,从而判断出复合命题的真假即可.
解答 解:sin(π-α)=sinα,当α=$\frac{π}{4}$时,sin(π-α)=sinα=cosα,
故命题p是真命题;
要使不等式ax2+ax+1>0的解集为R,
①当a=0时,1>0恒成立,满足条件;
②当a≠0时,满足$\left\{\begin{array}{l}{a>0}\\{{a}^{2}-4a<0}\end{array}\right.$,解得0<a<4,
因此要不等式ax2+ax+1>0的解集为R,必有0≤a<4,
故“0<a<4”是“ax2+ax+1>0的解集是实数集R”的充分不必要条件,
故命题q是假命题;
故p∧q”是假命题;
故选:C.
点评 本题考查了二次函数以及三角函数的性质,考查复合命题的判断,是一道基础题.


科目:高中数学 来源: 题型:选择题

| 指数 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
| 等级 | 一级优 | 二级良 | 三级轻度污染 | 四级中度污染 | 五级重度污染 | 六级严重污染 |
| A. | 6月份空气质量为优的天数为8天 | |
| B. | 6月份连续2天出现中度污染的概率为$\frac{2}{29}$ | |
| C. | 6月份北京空气质量指数AQI-PM2.5历史数据的众数为160 | |
| D. | 北京6月4至7日这4天的空气质量逐渐变好 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{15}}}{4}$ | B. | $-\frac{{\sqrt{15}}}{4}$ | C. | $\frac{1}{4}$ | D. | $-\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$?$\overrightarrow{b}$=$\overrightarrow{b}$?$\overrightarrow{a}$ | |
| B. | 若$\overrightarrow{a}$?$\overrightarrow{b}$=0,则$\overrightarrow{a}$$∥\overrightarrow{b}$ | |
| C. | ($\overrightarrow{a}$+$\overrightarrow{b}$)?$\overrightarrow{c}$=$\overrightarrow{a}$?$\overrightarrow{c}$+$\overrightarrow{b}$?$\overrightarrow{c}$ | |
| D. | 若$\overrightarrow{a}$=(x1,y1),$\overrightarrow{b}$=(x2,y2),则$\overrightarrow{a}$?$\overrightarrow{b}$=|x1y2-x2y1| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
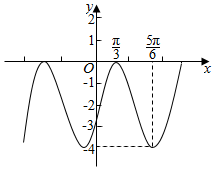 已知函数f(x)=sinωx(sinωx+2$\sqrt{3}$cosωx)+sin(ωx-$\frac{π}{4}$)sin(ωx+$\frac{π}{4}$)(其中ω为常数,且ω>0),函数g(x)=f(x)-$\frac{5}{2}$的部分图象如图所示.
已知函数f(x)=sinωx(sinωx+2$\sqrt{3}$cosωx)+sin(ωx-$\frac{π}{4}$)sin(ωx+$\frac{π}{4}$)(其中ω为常数,且ω>0),函数g(x)=f(x)-$\frac{5}{2}$的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x≤1} | B. | {x|-1<x<1} | C. | {x|-1≤x<1} | D. | {-1,1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com