
分析 根据凸函数和凹函数的定义,作出函数f(x)的图象,利用数形结合进行求解即可.
解答 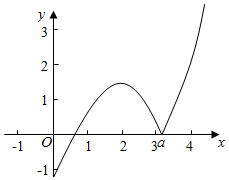 解:满足条件有$f(\frac{{{x_1}+{x_2}}}{2})>\frac{{f({x_1})+f({x_2})}}{2}$的函数为凸函数,
解:满足条件有$f(\frac{{{x_1}+{x_2}}}{2})>\frac{{f({x_1})+f({x_2})}}{2}$的函数为凸函数,
f(x)=$\left\{\begin{array}{l}{{x}^{2}-ax,}&{x≥a}\\{-{x}^{2}+ax,}&{x<a}\end{array}\right.$,作出函数f(x)的图象,
由图象知当x≤a时,函数f(x)为凸函数,当x≥a时,函数f(x)为凹函数,
若对任意x1∈[2,3],x2∈[2,3],x1≠x2恒有$f(\frac{{{x_1}+{x_2}}}{2})>\frac{{f({x_1})+f({x_2})}}{2}$,
则a≥3即可,
故实数a的取值范围是[3,+∞),
故答案为:[3,+∞)
点评 本题主要考查分段函数的应用,根据条件转化为凹函数和凸函数的定义,利用数形结合是解决本题的关键.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:选择题
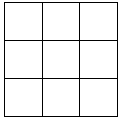 将4个红球与2个蓝球(这些球只有颜色不同,其他完全相同)放入一个3×3的格子状木柜里(如图所示),每个格至多放一个球,则“所有红球均不位于相邻格子”的放法共有( )种.
将4个红球与2个蓝球(这些球只有颜色不同,其他完全相同)放入一个3×3的格子状木柜里(如图所示),每个格至多放一个球,则“所有红球均不位于相邻格子”的放法共有( )种.| A. | 30 | B. | 36 | C. | 60 | D. | 72 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 110 | B. | 100 | C. | 90 | D. | 80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com