
分析 (1)可求得a1=2,a2=2+2λ,a3=2+6λ;从而可得2(2+2λ+1)=2+2+6λ,从而求λ;再利用累加法求通项公式;
(2)化简可得$\frac{p}{2n-5}$≤$\frac{16}{{2}^{n}}$,分类讨论,当n≥3时,P≤$\frac{16}{{2}^{n}}$(2n-5),从而判断当n≥4时,$\frac{16}{{2}^{n}}$(2n-5)随着n的增大而减小,从而求得.
解答 解:(1)∵a1=2,an+1=an+λ•2n,
∴a2=a1+λ•2=2+2λ,a3=a2+4λ=2+6λ;
∵a1,a2+1,a3成等差数列,
∴2(2+2λ+1)=2+2+6λ,
解得,λ=1;
故an+1-an=2n,
故a2-a1=2,a3-a2=4,…,an-an-1=2n-1,
故an-a1=2+4+8+…+2n-1=$\frac{2(1-{2}^{n-1})}{1-2}$=2n-2,
故an-2=2n-2,
故an=2n;
(2)∵$\frac{p}{2n-5}$≤$\frac{16}{{a}_{n}}$,∴$\frac{p}{2n-5}$≤$\frac{16}{{2}^{n}}$,
∵P>0,∴当n=1,2时,上式一定成立;
当n≥3时,P≤$\frac{16}{{2}^{n}}$(2n-5),
而$\frac{\frac{16}{{2}^{n+1}}(2n+2-5)}{\frac{16}{{2}^{n}}(2n-5)}$=$\frac{2n-3}{2(2n-5)}$=$\frac{1}{2}$+$\frac{1}{2n-5}$,
故当n≥4时,$\frac{1}{2}$+$\frac{1}{2n-5}$≤1,
故$\frac{16}{{2}^{n}}$(2n-5)随着n的增大而减小,
而$\frac{16}{8}$×1=2,$\frac{16}{16}$×3=3,$\frac{16}{32}$×5=2.5,
∵不等式$\frac{p}{2n-5}$≤$\frac{16}{{a}_{n}}$成立的自然数n恰有3个,
∴a1,a2,a4成立,
故p=3.
点评 本题考查了等差数列与等比数列的性质的判断与应用,同时考查了累加法的应用及方程思想与分类讨论的思想应用.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5}{6}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
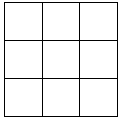 将4个红球与2个蓝球(这些球只有颜色不同,其他完全相同)放入一个3×3的格子状木柜里(如图所示),每个格至多放一个球,则“所有红球均不位于相邻格子”的放法共有( )种.
将4个红球与2个蓝球(这些球只有颜色不同,其他完全相同)放入一个3×3的格子状木柜里(如图所示),每个格至多放一个球,则“所有红球均不位于相邻格子”的放法共有( )种.| A. | 30 | B. | 36 | C. | 60 | D. | 72 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com