Question

4．某市营业区内住宅电话通话费为前3分钟0.20元（不足3分钟按3分钟计算），以后每分钟0.10元（不足1分钟按1分钟来计算）．
（1）在直角坐标系内，画出通话6分钟内（包括6分钟）的通话费y（元）关于通话时间t（分钟）的函数图象；

（2）如果一次通话t分钟（t＞0），写出通话费y（元）关于通话时间t（分钟）的函数关系式；（可用符号＜t＞表示不小于t的最小整数）
（3）如果通话时间较长，可以采用分若干次拨打电话的方法，某人通话91分钟，计算这个人用最省的时间的拨打方法比用一次拨打少花多少钱．

Answer 1

分析 （1）由题意可知话费分段收取，故利用分段函数作图即可；
（2）分3分钟内与超过3分钟分别写出函数表达式y=$\left\{\begin{array}{l}{0.2，0＜t≤3}\\{0.2+0.1＜t-3＞，t＞3}\end{array}\right.$；
（3）通话91分钟，用一次拨打时，y=0.2+0.1×（91-3）=9，通话91分钟，用最省钱的拨打方法时，y=02×$\frac{90}{3}$+0.1=6.1，从而比较即可．

解答 解：（1）作图如下，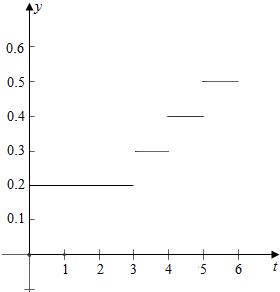

（2）y=$\left\{\begin{array}{l}{0.2，0＜t≤3}\\{0.2+0.1＜t-3＞，t＞3}\end{array}\right.$；
（3）通话91分钟，用一次拨打时，y=0.2+0.1×（91-3）=9，
通话91分钟，用最省钱的拨打方法时，y=02×$\frac{90}{3}$+0.1=6.1；
故少花9-6.1=2.9元，
故这个人用最省的时间的拨打方法比用一次拨打少花2.9元．

点评 本题考查了分段函数在实际问题中的应用，属于中档题．