
| A. | 9 | B. | 13 | C. | 17 | D. | 21 |
分析 利用三角函数的图象与性质求出f(f(x))=0的解的个数;借助函数图象判断f(g(x))=0和g(g(x))=0的解的个数.
解答 解:(1)令f(x)=|sinx|=0得x=kπ,k∈{-1,0,1},
又f(x)=|sinx|的值域为[0,1],f(f(x))=0,
∴f(x)=0,∴x=kπ,k∈{-1,0,1}.
∴f(f(x))=0有3个根,即m=3.
(2)∵f(g(x))=0,
∴g(x)=kπ,k∈{-1,0,1},
①若g(x)=0,则$\frac{1}{2}$x=sinx,作出y=$\frac{1}{2}$x和y=sinx的函数图象如图所示:
由图象可知g(x)=0在[-π,π]上有3个解,
②若g(x)=π,则$\frac{1}{2}$x=sinx+$\frac{π}{2}$,作出y=$\frac{1}{2}$x和y=sinx+$\frac{π}{2}$的函数图象如图所示: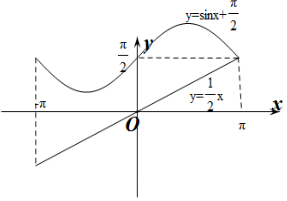
由图象可知g(x)=0在[-π,π]上只有1个解,
③同理可得:当g(x)=-π在[-π,π]上只有1个解,
∴f(g(x))=0的根的个数为5,即n=5.
(3)由(2)中的第①种情况可知g(x)=0有3解,不妨设为x1,x2,x3,且x1<x2<x3,
则x1+x3=0,x2=0,且$\frac{π}{2}$<x3<π,
∵g(g(x))=0,∴g(x)=xi,i=1,2,3.
①若g(x)=x2=0,则g(x)=0有3解,
②若g(x)=x3,则$\frac{1}{2}x$=sinx+$\frac{1}{2}{x}_{3}$,
设y=sinx+b(b>0)与直线y=$\frac{1}{2}$x相切,切点为(x0,y0),则$\left\{\begin{array}{l}{cos{x}_{0}=\frac{1}{2}}\\{\frac{1}{2}{x}_{0}=sin{x}_{0}+b}\end{array}\right.$,
解得b=$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$,∵$\frac{1}{2}{x}_{3}$>$\frac{π}{4}$>b,
∴g(x)=x3只有1解,
③同理可得:g(x)=x1只有1解;
∴g(g(x))=0共有5个解,即t=5.
∴m+n+t=13.
故选B.
点评 本题考查了函数零点与函数图象的关系,函数图象的变换,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | cos201.2° | B. | -cos201.2° | C. | sin201.2° | D. | tan201.2° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,4] | B. | [2,6] | C. | [3,7] | D. | $[2\sqrt{2},4\sqrt{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
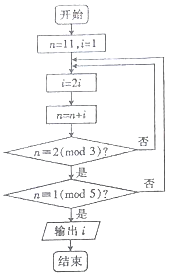 若正整数N除以正整数m后的余数为n,则记为N=n(mod m),例如10=2(mod 4),下面程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的i等于( )
若正整数N除以正整数m后的余数为n,则记为N=n(mod m),例如10=2(mod 4),下面程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的i等于( )| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 108种 | B. | 102种 | C. | 18种 | D. | 20种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
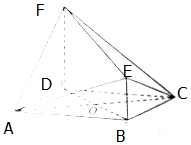 如图,在几何体ABCDEF中,四边形ABCD是菱形,BE⊥平面ABCD,DF∥BE,且DF=2BE=2,EF=3.
如图,在几何体ABCDEF中,四边形ABCD是菱形,BE⊥平面ABCD,DF∥BE,且DF=2BE=2,EF=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 班级 | 高三(1) | 高三(2) | 高三(3) |
| 人数 | 3 | 3 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com