
【题目】已知椭圆![]() 中心在原点,焦点在
中心在原点,焦点在![]() 轴上,且其焦点和短轴端点都在圆
轴上,且其焦点和短轴端点都在圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)点![]() 是圆
是圆![]() 上一点,过点
上一点,过点![]() 作圆
作圆![]() 的切线交椭圆
的切线交椭圆![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)2
;(2)2
【解析】
(1)由题意设出椭圆的标准方程,由于椭圆焦点和短轴端点都在圆![]() :
:![]() 上,可得到
上,可得到![]() ,
,![]() 的值,即可求出椭圆方程。
的值,即可求出椭圆方程。
(2)分类讨论切线方程斜率存在与不存在的情况,当斜率不存在时,可直接确定![]() 的值,再讨论斜率存在时,设出直线方程与椭圆方程联立,利用韦达定理表示出
的值,再讨论斜率存在时,设出直线方程与椭圆方程联立,利用韦达定理表示出![]() ,再结合直线与圆相切性质消去一个参数,利用函数的单调性确定
,再结合直线与圆相切性质消去一个参数,利用函数的单调性确定![]() 的范围,最后得到
的范围,最后得到![]() 的最大值。
的最大值。
(1)由椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,故设椭圆
轴上,故设椭圆![]() 的标准方程为
的标准方程为![]() ,
,
![]() 椭圆的右焦点坐标为
椭圆的右焦点坐标为![]() ,上顶点坐标为
,上顶点坐标为![]()
![]() 椭圆
椭圆![]() 焦点和短轴端点都在圆
焦点和短轴端点都在圆![]() :
:![]() 上,
上,
![]()
![]() ,
,![]() ,解得:
,解得:![]() ,
,![]() ,
,
![]()
![]() ,即
,即![]() ,
,
椭圆![]() 的标准方程为
的标准方程为![]()
(2)当切线![]() 的斜率不存在时,切线方程为:
的斜率不存在时,切线方程为:![]() ,与椭圆
,与椭圆![]() 的两个交点为
的两个交点为![]() 或
或![]() ,则
,则![]() ,
,
当切线![]() 的斜率存在时,设切线方程为:
的斜率存在时,设切线方程为:![]() ,切线与椭圆交点的坐标分别为
,切线与椭圆交点的坐标分别为![]() ,
,![]() ,
,
联立方程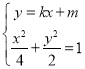 ,得:
,得:![]() ,
,
由于切线与椭圆相交于两点,则![]() ,
,
由韦达定理可得: ,
,
又![]() 直线
直线![]() 与圆
与圆![]() 相切,
相切,
![]()
![]() ,即
,即![]() ,
,
![]()
![]()
![]()
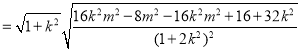




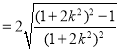
![]()
令![]() ,则函数
,则函数![]() 单调递增,当
单调递增,当![]() ,
,![]()
![]()
![]() ,
,
综上所述,![]()


科目:高中数学 来源: 题型:
【题目】装有除颜色外完全相同的6个白球、4个黑球和2个黄球的箱中随机地取出两个球,规定每取出1个黑球赢2元,而每取出1个白球输1元,取出黄球无输赢.
(1)以X表示赢得的钱数,随机变量X可以取哪些值?求X的分布列;
(2)求出赢钱(即![]() 时)的概率.
时)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列“若p,则q”形式的命题中,哪些命题中的q是p的必要条件?
(1)若四边形为平行四边形,则这个四边形的两组对角分别相等;
(2)若两个三角形相似,则这两个三角形的三边成比例;
(3)若四边形的对角线互相垂直,则这个四边形是菱形;
(4)若![]() ,则
,则![]() ;
;
(5)若![]() ,则
,则![]() ;
;
(6)若![]() 为无理数,则x,y为无理数.
为无理数,则x,y为无理数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区农产品近几年的产量统计如下表:

为了研究计算的方便,工作人员将上表的数据进行了处理,![]() 得到下表:
得到下表:

(1)根据表中数据,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若近几年该农产品每万吨的价格![]() (万元)与年产量
(万元)与年产量![]() (万吨)满足
(万吨)满足![]() ,且每年该农产品都能售完,当年产量
,且每年该农产品都能售完,当年产量![]() 为何值时,销售额
为何值时,销售额![]() 最大?
最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分別为:
的斜率和截距的最小二乘估计分別为: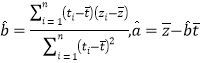 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三角形的三个顶点的坐标分别为![]() ,
,![]() ,
,![]() ,则该三角形的重心(三边中线交点)的坐标为
,则该三角形的重心(三边中线交点)的坐标为![]() .类比这个结论,连接四面体的一个顶点及其对面三角形重心的线段称为四面体的中线,四面体的四条中线交于一点,该点称为四面体的重心.若四面体的四个顶点的空间坐标分别为
.类比这个结论,连接四面体的一个顶点及其对面三角形重心的线段称为四面体的中线,四面体的四条中线交于一点,该点称为四面体的重心.若四面体的四个顶点的空间坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() ,则该四面体的重心的坐标为( )
,则该四面体的重心的坐标为( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高一学年结束后,要对某班的50名学生进行文理分班,为了解数学对学生选择文理科是否有影响,有人对该班的分科情况做了如下的数据统计:
理科人数 | 文科人数 | 总计 | |
数学成绩好的人数 | 25 | 30 | |
数学成绩差的人数 | 10 | ||
合计 | 15 |
(Ⅰ)根据数据关系,完成![]() 列联表;
列联表;
(Ⅱ)通过计算判断能否在犯错误的概率不超过![]() 的前提下认为数学对学生选择文理科有影响.
的前提下认为数学对学生选择文理科有影响.
附:![]()
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
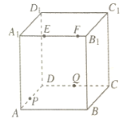
【题目】如图,正方体![]() 的棱长为4,动点E,F在棱
的棱长为4,动点E,F在棱![]() 上,动点P,Q分别在棱AD,CD上。若
上,动点P,Q分别在棱AD,CD上。若![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() 大于零),则四面体PEFQ的体积
大于零),则四面体PEFQ的体积
A.与![]() 都有关B.与m有关,与
都有关B.与m有关,与![]() 无关
无关
C.与p有关,与![]() 无关D.与π有关,与
无关D.与π有关,与![]() 无关
无关
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com